| Главная Научный калькулятор | |
|
|
Геометрическая прогрессияГеометрическая прогрессияПоследовательность (аn), у которой а1=а и для любого nаn+1=an * q (1),
где а и q любые отличные от нуля заданные числа, называется геометрической прогрессией. Число q называется знаменателем геометрической прогрессии.Если а>0 и q>1, то геометрическая прогрессия является возрастающей последовательностью, если же а>0 и 0<q<1, то геометрическая прогрессия убывающая. Очевидно, что при а<0, наоборот, геометрическая прогрессия убывающая, если q>1, и возрастающая, если 0<q<1. При q<0 каждый член прогрессии имеет знак, противоположный знаку последующего члена, она не будет монотонной. Формула для n-го члена геометрической прогрессии имеет вид аn=аqn-1 (2)
Докажем её методом математической индукции. Формула (2), очевидно, верна при n=1. Предположим, что она верна и при n=k+1, т.е. ak=aqk-1. Из (1) следует ak+1=aqk. Подставляя сюда выражения для k-го члена, получаем
ak+1=aqk, то есть формула (2) справедлива при n=k+1. Из принципа математической индукции следует, что формула (2) верна для любого натурального n.Геометрическая прогрессия, содержащая конечное число членов, называется конечной геометрической прогрессией. Свойства геометрической прогрессии- I. Квадрат каждого члена геометрической прогрессии, начиная со второго, равен произведению соседних членов, т.е. при k≥2 ak2=ak-1 * ak+1 (3)
Если все члены геометрической прогрессии положительны, то это свойство формулируется так: Каждый член геометрической прогрессии, начиная со второго, равен среднему геометрическому его соседних членов, т.е. при k≥2
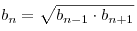 аk * an-k+1=a1 * an (4)
- III. Если знаменатель геометрической прогрессии q не равен единице и Sn=a1+a2+...+an, то
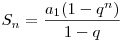 (5) (5)Sn=a+aq+...+aqn-1 (6)
тогда
qSn=aq+aq2+...+aqn (7)
Вычитая почленно из равенства (6) равенство (7), получим
(1-q)Sn=a(1-qn), (8)
откуда при q не равном единице следует формула (5).
|