| Главная Научный калькулятор | |
|
|
Усеченный конус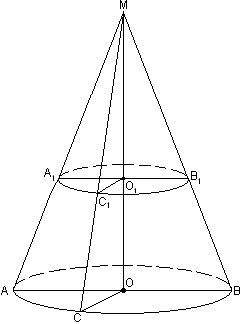 Теорема 4. Всякое сечение конуса, параллельное его основанию и не проходящее через его вершину, есть круг. Высота конуса проходит через его центр. Доказательство. Высота конуса будет перпендикулярна плокости сечения, т.к. если прямая перпендикулярна одной из параллельных прямых, то она перпендикулярна и другой. Обозначим точку пересечения высоты и плокости сечения за О1. Тогда МО1 будет перпендикулярна О1А1, О1В1 и О1С1, а треугольники МО1А1, МО1В1 и МО1С1 являются прямоугольными. Они равны по катету и острому углу (МО1 - общая, углы при вершине М равны, что следует из равенства треугльников МОА, МОВ и МОС по двум катетам (МО - общая, ОА=ОВ=ОС - радиусы основания)).
Поэтому равны соответственные катеты и гипотенузы. Значит, точка О1 равноудалена от всех точек линии сечения, что определяет её (линию сечения) как окружность, ну а фигура ей ограниченная есть круг. Ч.т.д.
Теорема 4. Всякое сечение конуса, параллельное его основанию и не проходящее через его вершину, есть круг. Высота конуса проходит через его центр. Доказательство. Высота конуса будет перпендикулярна плокости сечения, т.к. если прямая перпендикулярна одной из параллельных прямых, то она перпендикулярна и другой. Обозначим точку пересечения высоты и плокости сечения за О1. Тогда МО1 будет перпендикулярна О1А1, О1В1 и О1С1, а треугольники МО1А1, МО1В1 и МО1С1 являются прямоугольными. Они равны по катету и острому углу (МО1 - общая, углы при вершине М равны, что следует из равенства треугльников МОА, МОВ и МОС по двум катетам (МО - общая, ОА=ОВ=ОС - радиусы основания)).
Поэтому равны соответственные катеты и гипотенузы. Значит, точка О1 равноудалена от всех точек линии сечения, что определяет её (линию сечения) как окружность, ну а фигура ей ограниченная есть круг. Ч.т.д.Плоскость сечения разбивает конус на два тело. Верхнее является конусом по определению, а нижнее есть усеченный конус. Определение 6. Усеченный конус - тело, образованное сечением конуса плокостью, параллельной его основанию и не проходящей через его вершину, заключенное между плокостью основания и плокостью сечения. Формула объема усеченного конуса следует из формула объеа усеченной пирамиды, доказанной здесь. Эта формула, как видно из её вывода, остается верна и для конуса. Если даны радиусы R1 и R2 оснований усеченного конуса, то S1=pR12, S2=pR22, и формула примет вид Теорема 5. Объем усеченного конуса определяется по формуле Также выводится и формула площади усеченного конуса, т.к. формула площади боковой поверхности правильной усеченной пирамиды остается верной (вывод не изменится) и для усеченного конуса. Если радиусы оснований R1 и R2, а образующая - l, то получаем Теорема 6. Площадь боковой поверхности усеченного конуса определяется по формуле Sбок=pl(R1+R2) |