| Главная Научный калькулятор | |
|
|
Медианы и высоты треугольникаОпределение 5. Медианой треугольника называют отрезок, соединяющий вершину треугольника с серединой противолежащей стороны. Также под медианой иногода понимается вся прямая, на которой лежит этот отрезок. Треугольник имеет три медианы, соответственно соединяющие три вершины и три его стороны.Теорема 11. Медианы треугольника пересекаются в одной точке и точкой пересечения делят друг друга в отношении 2:1, считая от вершины. 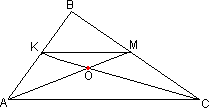 Доказательство. Для начала рассмотрим две медианы АМ и СК. КМ является средней линией по определению. Поэтому отрезок КМ параллелен АС. Значит, соответственно равны углы АМК и МАС; СКМ и КСА. Поэтому треугольники АОС и КОМ подобны по двум углам. Также мы знаем, что средняя линия треугольника равна половине той стороны, которой она параллельна, т.е. КМ=1/2АС или АС=2КМ. Из подобия вытекают следующие соотношения:
Доказательство. Для начала рассмотрим две медианы АМ и СК. КМ является средней линией по определению. Поэтому отрезок КМ параллелен АС. Значит, соответственно равны углы АМК и МАС; СКМ и КСА. Поэтому треугольники АОС и КОМ подобны по двум углам. Также мы знаем, что средняя линия треугольника равна половине той стороны, которой она параллельна, т.е. КМ=1/2АС или АС=2КМ. Из подобия вытекают следующие соотношения:АО:ОМ=СО:ОК=АС:КМ=2КМ:КМ=2:1, т.е. в точке О эти медианы поделились в данном отношении. 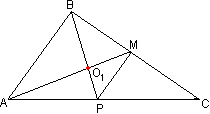 Теперь рассмотрим этот рисунок. Подобными доказательствами придем к следующему:
Теперь рассмотрим этот рисунок. Подобными доказательствами придем к следующему:АО1:О1М=ВО1:О1Р=АВ:РМ=2РМ:РМ=2:1, т.е. в точке О1 эти медианы поделились в данном отношении. Т.е. и точка О, и точка О1 делят медиану АМ в одинаковом отношении, а значит они совпадают в одну точку - точку пересечения всех трех медиан треугольника, делящую их в отношении 2:1 считая от вершин. Точка пересечения медиан треугольника является его центром тяжести. Это значит, что именно в точке пересечения медиан помещается центр тяжести тонкой однородной пластинки треугольной формы. Определение 6. Высотой треугольника называется перпендикуляр, опущенный из его вершины на прямую, которая содержит противолежащую сторону треугольника. Высотой также называется длина этого перпендикуляра. 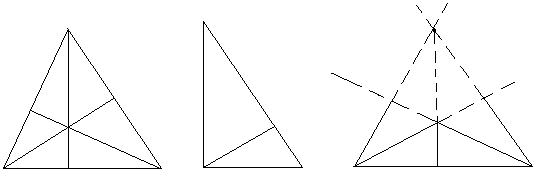 Треугольник имеет три высоты. В случае остроугольного треугольника высоты располагаются внутри его. У прямоугольного треугольника две высоты совпадают с его катетами, третья же сторона, опущенная из вершины острого угла на гипотенузу, лежит внутри треугольника. Наконец, у тупоугольного треугольника две его высоты, проведенные из вершин острых углов, лежат вне треугольника, их основания помещаются на продолжениях сторон. Теорема 12. Три высоты любого треугольника пересекаются в одной точке. 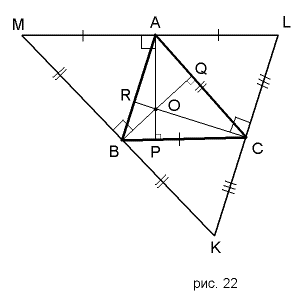
Доказательство: Пусть ABC - данный треугольник (рис. 22). Пусть прямые, содержащие высоты AP и BQ треугольника ABC пересекаются в точке O. Проведем через точку A прямую, параллельную отрезку BC, через точку B прямую, параллельную отрезку AC, а через точку C - прямую, параллельную отрезку AB. Все эти прямые попарно пересекаются. Пусть точка пересечения прямых, параллельных сторонам AC и BC - точка M, точка пересечения прямых, параллельных сторонам AB и BC - точка L, а прямых, параллельным AB и AC - точка K. Точки KLM не лежат на одной прямой, (иначе бы прямая ML совпадала бы с прямой MK, а значит, прямая BC была бы параллельна прямой AC, или совпадала бы с ней, то есть точки A, B и C лежали бы на одной прямой, что противоречит определению треугольника). Итак, точки K, L, M составляют треугольник. MA параллельно BC, и MB параллельно AC по построению. А значит, четырёхугольник MACB - параллелограмм. Следовательно, MA = BC, MB = AC. Аналогично AL = BC = MA, BK = AC = MB, KC = AB = CL. Значит, AP и BQ - серединные перпендикуляры к сторонам треугольника KLM. Они пересекаются в точке O, а значит, CO - тоже срединный перпендикуляр. CO перпендикулярно KL, KL параллельно AB, а значит CO перпендикулярно AB. Пусть R - точка пересечения AB и CQ. Тогда CR перпендикулярно AB, то есть CR - это высота треугольника ABC. Точка O принадлежит всем прямым, содержащим высоты треугольника ABC. Значит, прямые, содержащие высоты этого треугольника пересекаются в одной точке. Что и требовалось доказать. |