| Главная Научный калькулятор | |
|
|
Задача №110Основанием пирамиды является параллелограмм, стороны которого равны 20 см и 36 см, а площадь равна 360см2. Высота пирамиды проходит через точку пересечения диагоналей основания и равна 12 см. Найдите площадь боковой поверхности пирамиды.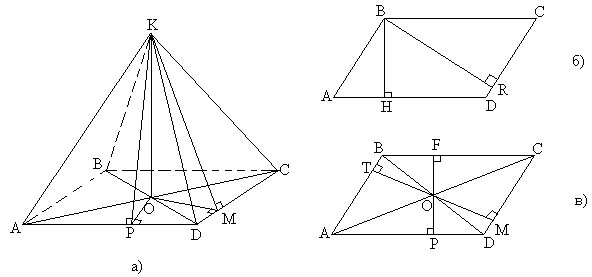 Запишем формулу площади параллелограмма для высоты ВН и стороны AD: S=ВН*AD 36ВН=360 ВН=10 Запишем формулу площади параллелограмма для высоты ВR и стороны CD: S=ВR*CD 20ВR=360 ВR=18 Прямоугольные треугольники АРО и OFC равны по гипотенузе и острому углу: АО=ОС (диагонали точкой пересечения делятся попалам), углы ОАР и ОСF равны (накрест лежащие при параллельных прямых AD и ВС и секущей АС). Это означает, что OP=OF=1/2PF=1/2BH=5 Также и для треугольников ОТВ и ОМD: ОТ=ОМ=1/2TM=1/2BR=9 Соединим точки М и К (рис а). Прямая МК перпендикулярна СD по теореме о трех перпендикулярах. Из прямоугольного треугольника КОМ определим КМ по теореме Пифагора: КМ=15 Также соединим точки Р и К (рис а). Прямая РК перпендикулярна АD по теореме о трех перпендикулярах. Из прямоугольного треугольника КОР определим КР по теореме Пифагора: КР=13 Противоположные боковые грани пирамиды равны (по трем сторонам: у параллелограмма противоположные стороны равны, все боковые ребра данной пирамиды равны), а значит равны и их площади. Поэтому формулу площади боковой поверхности запишем так: Sбок=2SAKD+2SCKD Sбок=2*1/2*AD*KP+2*1/2*DC*KM Sбок=36*13+20*15=768 |