| Главная Научный калькулятор | |
|
|
Задача №127Основание пирамиды SABC-прямоугольный треугольник, катеты CA и CB равны a, боковое ребро SC перпендикулярно основанию и тоже равно a. Найти R сферы, вписанной в эту пирамиду.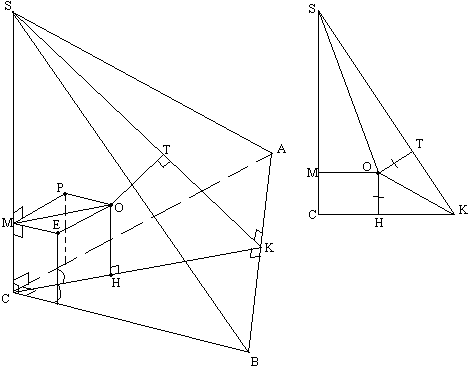 Раз два катета равны, значит этот прямоугольный треугольник равнобедренный. Проведем в нем высоту СК. По о трех перпендикулярах. Плоскость KSС является биссекторной для двугранного угла при ребре CS, т.к. проходит через это ребро и биссектрису СК линейного угла этого двугранного угла. Теорема. Центр вписанной в пирамиду сферы лежит на пересечении биссекторных плоскостей двугранных углов при каждом ребре этой пирамиды. Поэтому точка О - центр вписанной сферы лежит где-то в плоскости KSС. Плоскость KSС перпендикулярна плоскости основания пирамиды АВС, т.к. проходит через ребро SС, перпендикулярное АВС. Также плоскость KSС перпендикулярна плоскости ABS, т.к. плоскость ABS проходит через ребро АВ, перпендикулярное плоскости KSС (прямая тогда перпендикулярна плоскости, когда она перпендикулярна двум пересекающимся прямым этой плоскости, а как было доказано АВ перпендикулярна SК и СК). Теорема. Если из точки, лежащей в одной из двух перпендикулярных плоскостей, опустить перпендикуляр на другую, то этот перпендикуляр упадет на линию пересечения этих плоскостей. Поэтому перпендикуляр, опущенный из точки О на плоскость АВС упадет на прямую СК, а на плоскость SАВ на прямую SK. Из точки О опустим перпендикуляр ОР на плоскось SСВ. Теперь из точки Р опустим перпендикуляр РМ на ребро CS. Соединим точки М и О. МО перпендикулярна ребру CS по теореме о трех перпендикулярах (МО - наклонная; РМ - проекция). Теперь из точки О опустим перпендикуляр ОЕ на плоскось SСА. Соединим точки Е и М. ЕМ перпендикулярна ребру CS по теореме о трех перпендикулярах (МО - наклонная; ЕМ - проекция). Угол ЕМР - линейный угол двугранного угла между плоскостями SCB и SCA, а он равен 90 градусов, т.к. угол АСВ прямой. Поэтому прямая ЕМ перпендикулярна плоскости CSB (ЕМ перпендикулярна CS и MP). Прямые ЕМ и ОР параллельны, т.к. перпендикулярны одной и той же плоскости CSB. Проведем через них плоскость. Четырехугольник ОРМЕ - квадрат (в нем все углы прямые и ОР=ОЕ как радиусы), значит все стороны в нем равны. Обозначим радиус вписанной сферы за R. Из прямоугольного треугольника ОРМ найдем ОМ: ОН=ОТ=R СВ=СА=СS=а, следовательно прямоугольные треугольники SCB и SCA равны по двум катетам, и поэтому равны их гипотенузы SA и SB: Из треугольника АВС: Теперь взглянем на правый рисунок. В четырехугольнике МОНС противоположные стороны параллельны, т.к. (МО и СН) и (МС и ОН) соответственно перпендикулярны одной и той же прямой СS и СК. Также в этом четырехугольнике хотябы один из углов равен 90 градусов. Поэтому он является прямоугольником. Значит, МО = СН и МС = ОН. НК=СК-СН. Прямоугольные треугольники ОНК и ОТК равны по катету и гипотенузе (ОК - общая, ОН=ОТ=R), поэтому ТК=НК=СК-СН. ST=SK-TK=SK-(СК-СН)=SK-СК+СН SM=SC-MC Теперь для треугольников SOM и SOT запишем теорему Пифагора: 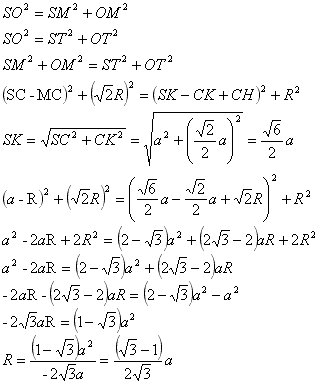
|