| Главная Научный калькулятор | |
|
|
Задача №130Отрезок BD - диаметр окружности центра О. Хорда АС делит радиус ОВ пополам и перпендикулярна к нему. Найти углы четырёхугольника АBCD.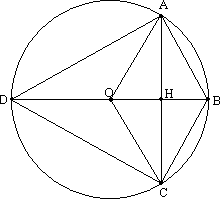 Ознакомьтесь с темами четырехугольник здесь Исходя из теоремы: перпендикуляр (ОН), опущенный на хорду (АС) из центра окружности, делит эту хорду пополам и условий задачи замечаем, что четырехугольник ОАВС - ромб (если в четырехугольнике диагонали перпендикулярны и точкой пересечения делятся попалам, то он ромб). Поэтому углы АОС и АВС равны. Исходя из теоремы: величина вписанного угла (ADC) равна половине угловой величины дуги (АОС), на которую он опирается, получаем ∠АОС=2∠ADC=∠АВС Зная, что у любого четырехугольника, вписанного в окружность, суммы пар противоположных углов равны 180о, запишем: 2∠ADC+∠АВС=3∠ADC=180о ∠ADC=60о ∠АВС=2∠ADC=120о Зная, замечание о том, что вписанный в окружность угол, опирающийся на диаметр, равен 90о, заключам, что: ∠А=∠С=90о |