| Главная Научный калькулятор | |
|
|
Задача №137При пересечении двух окружностей образуется хорда АВ. На продолжении этой хорды ставим точку М. Доказать что касательные проведенные из точки М к окружностям равны.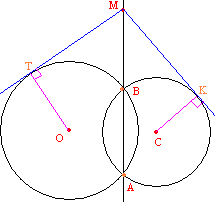 Вспомним теорему 10 из темы круг и окружность: Если из точки к окружности проведены касательная и секущая, то квадрат отрезка касательной от данной точки до точки касания равен произведению длин отрезков секущей от данной точки до точек её пересечения с окружностью. Применим эту теорему для касательной МТ и секущей МА: МТ2=МА*МВ. Теперь применим эту теорему для касательной МК и секущей МА: МК2=МА*МВ. Значит, МТ2=МК2 и МТ=МК, ч.т.д |