|
|
|
Главная
Научный калькулятор
|
|
|
Задача №142
Даны две внутрекасающиеся окружности (т.е. одна находится внутри другой, при этом они имеют одну общую точку).
Требуется доказать, что точка касания и центры окружностей лежат на одной прямой.
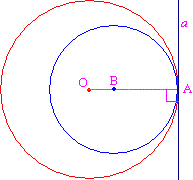
Через точку А касания окружностей проведем касательную к большей окружности. Эта прямая является также касательной и для меньшей окружности, т.к. имеет с ней только одну точку. Теперь из центров окружностей О и В проведем радиусы в точку касания. Как известно, радиус, проведенный в точку касания, перпендикулярен касательной. Мы имеем на плоскости из одной точки А восстановлено два перпендикуляра АО и АВ, чего быть не может, поэтому прямые АО и АВ совпадают и точки О В и А лежат на одной прямой.
|
 Через точку А касания окружностей проведем касательную к большей окружности. Эта прямая является также касательной и для меньшей окружности, т.к. имеет с ней только одну точку. Теперь из центров окружностей О и В проведем радиусы в точку касания. Как известно, радиус, проведенный в точку касания, перпендикулярен касательной. Мы имеем на плоскости из одной точки А восстановлено два перпендикуляра АО и АВ, чего быть не может, поэтому прямые АО и АВ совпадают и точки О В и А лежат на одной прямой.
Через точку А касания окружностей проведем касательную к большей окружности. Эта прямая является также касательной и для меньшей окружности, т.к. имеет с ней только одну точку. Теперь из центров окружностей О и В проведем радиусы в точку касания. Как известно, радиус, проведенный в точку касания, перпендикулярен касательной. Мы имеем на плоскости из одной точки А восстановлено два перпендикуляра АО и АВ, чего быть не может, поэтому прямые АО и АВ совпадают и точки О В и А лежат на одной прямой.