| Главная Научный калькулятор | |
|
|
Задача №146В правильную треугольную пирамиду вписан шар. Высота пирамиды пересекает шар в точке М. Площадь сечения шара плоскостью проходщей через сторону пирамиды и точку М относится ко всей площади пов. шара как 3:19. Найти косинус угла между боковой гранью пирамиды и ее основанием.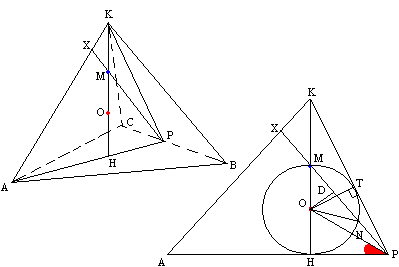 Как известно высота правильной пирамиды падает в середину основания. Центр треугольника есть точка пересечения медиан. В нашем случае треугольник правильный, поэтому все медианы, высоты и биссектрисы совпадают. Проведем например медиану (высоту, биссектрису) АР. Соединим точки Р и К. РК перпендикулярна ВС по следствию третей аксиомы. Центр вписанного в правильную пирамиду шара лежит на её высоте.
Как известно высота правильной пирамиды падает в середину основания. Центр треугольника есть точка пересечения медиан. В нашем случае треугольник правильный, поэтому все медианы, высоты и биссектрисы совпадают. Проведем например медиану (высоту, биссектрису) АР. Соединим точки Р и К. РК перпендикулярна ВС по следствию третей аксиомы. Центр вписанного в правильную пирамиду шара лежит на её высоте. Проведем плоскость через точку М и ребро ВС. Для этого продолжим РМ до пересечения с АК, а заием точку Х соединим с точками В и С. Плоскость ХВС и есть искомая плоскость. Рассмотрим плоскость АКР. Любое сечение шара плоскостью есть круг. Проведем в полученном круге радиус перпендикулярно хорде MN. Он разделит эту хорду пополам (по теореме 1 из темы круг и окружность). Обозначим MD=DN=r, радиус круга за R. Обозначим угол ОРН за α. Запишем некоторые соотношение и опишем их: 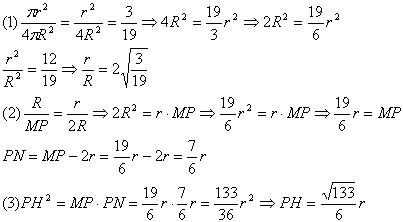 уравнение 1 - данные задачи: Площадь сечения шара плоскостью проходщей через сторону пирамиды и точку М относится ко всей площади пов. шара как 3:19. уравнение 2 - из подобия прямоугольных треугольников МРН и МDО (по острому углу) уравнение 3 - по теореме 10 из темы круг и окружность Точка О удалена от сторон РН и РК (ОН=ОТ - радиусы), поэтому РО является биссектрисой угла КРН, т.е. ∠ОРН=∠ОРТ=α. Найдем котангенс угла ОРН  Здесь уравнение 4 - формула половинного угла для котангенса. Нужно заметить, что ∠КРН=2α Здесь уравнение 4 - формула половинного угла для котангенса. Нужно заметить, что ∠КРН=2α
|