Задача №196

Из точки М проведен перпендикуляр МD, равный 6 см., к плоскости квадрата АВСD. Наклонная МВ образует с плоскостью квадрата угол 60°. Доказать, что треугольники МАВ и МСВ прямоугольные. Найдите сторону квадрата. Докажите, что треугольник АВD является проекцией треугольника МАВ на плоскость квадрата, и найдите его площадь.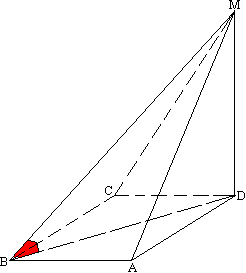
Угол между прямой и плоскостью - это угол между этой прямой и её проекцией на эту плоскость. Т.е. ∠МВD=60°.
Рассмотрим наклонную МС, проекцию CD и прямую в проскости ВС. Угол ВСD прямой (угол квадрата). По теореме о трех перпендикулярах угол МСВ тоже равен 90 градусов. А треугольник МСВ прямоугольный. Аналогично треугольник МАВ тоже является прямоугольным.
MD перпендикулярна плоскости квадрата, а значит перпендикулярна и любой прямой (BD к примеру) в этой плоскости. Рассмотрим прямоугольный треугольник МВD. В нем:
BD=MD * ctg60°
BD=6 * (корень из 3)/3 BD=2 корня из 3
Известно, что диагональ квадтрата больше его стороны в корень из 2 раз, поэтому:
АВ=BD/(корень из 2)
АВ=(2 корня из 3)/(корень из 2)=корень из 6

Две вершины треугольника АМВ уже лежат в плоскости АВСD, а точка М ортогонально спроектировна в точку D. Поэтому треугольник АBD является проекцией треугольника АМВ. S_ABD=1/2 * АВ²=3