Задача №21

Найдите объем V треугольной пирамиды, если все её боковые рёбра равны l, а стороны основания равны a, b и c.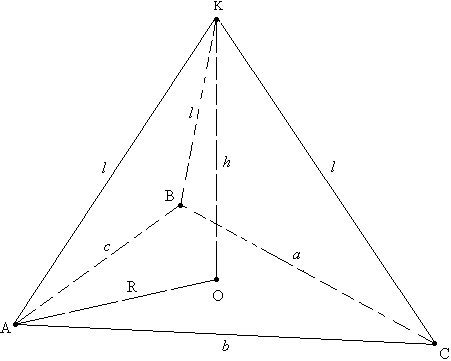
Вспомним теорему: Если все боковые ребра пирамиды равны, то высота, опущенная из вершины на основание, падает в центр описанной около основания окружности.
Обозначим радиус описанной около основания окружности за R.
Для определения площади основания применим формулу Герона:

Теперь определим АО как радиус описанной около основания окружности:

Высота КО перпендикулярна основанию АВС, т.е. перпендикулярна и любой прямой этой плоскости (по определению, например, прямой АО. Это в свою очередь означает, что треугольник КОА прямойгольный. По теореме Пифагора найдем в нем катет КО - высоту пирамиды:

подставим значение R:

Теперь найдем объем по известным высоте и площади основания: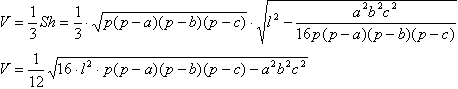

Используя математические преобразования можно получить следующую форумулу, которая пригодится в случае, когда значения длин сторон иррациональны: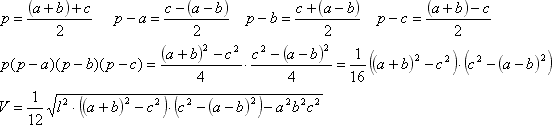