| Главная Научный калькулятор | |
|
|
Задача №216Дана правильная треугольная призма ABCA1B1C1. AB=2, угол между плоскостью ABC и плоскостью BCF равен 45 градусов. F- середина AA1. Найти площадь боковой поверхности!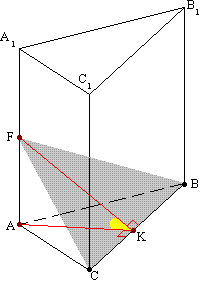 Соединим соответственно точки В и F, С и F, чтобы получить плоскость ВСF.
Соединим соответственно точки В и F, С и F, чтобы получить плоскость ВСF.Раз призма правильная, то её основанием является правильный треугольник сто стороной 2, а боковые ребра перпендикулярны основанию. Боковое ребро перпендикулярно основанию АВС. Поэтому оно перпендикулярно и АК (по определению перпендикуляра к плоскости). В плоскости основания АВС проведем высоту АК. Теперь соединим точки К и F. KF перпендикулярна ВС по теореме о трех перпендикулярах. Угол АКF является линейным углом двугранного угла между плоскостями АВС и ВСF, поэтому он равен 45°. Найдем высоту АК в треугльнике АВС: Из прямоугольного треугольника АКF найдем катет АF, а затем и все ребро АА1: Теперь найдем площадь боковой поверхности по формуле площади боковой поверхности правильной призмы: где Р - периметр основания АВС, l - боковое ребро. |