| Главная Научный калькулятор | |
|
|
Задача №223Стороны прямоугольника равны 5 и 4 см. Биссектрисы углов, прилегающих к боковой стороне, делят противоположную сторону на 3 части. Найти длины этих частей.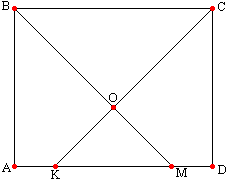 Вообще в прямоугольнике любые две противоположные стороны можно принять за боковые, но можно видеть, что биссектрисы, проведенные из углов, прилегающих к сторонам АВ и CD не пересекают соответственно противоположные стороны в пределах отрезков CD и АВ. Поэтому рассмотрим стороны ВС и AD. Можно рассматривать два пункта решения в зависимости от того, к какой стороне прилегают углы, из которых будем проводить биссектрисы, но ясно, что нет разницы какую сторону рассмотрим, ведь соответственно противоположная сторона будет разбита одинаково. Итак, рассмотрим сторону ВС, а именно углы, прилегающие к ней. Проведем биссектрисы ВМ и СК. Как известно биссектриса разбивает угол пополам, поэтому ∠АВМ=45° и ∠КСD=45°. Следовательно, прямоугольные треугольники АВМ и KCD равнобедренные и АВ=АМ=4, CD=KD=4, откуда АК=AD-KD=5-4=1 MD=AD-AM=5-1=1 MK=AD-AK-MD=5-1-1=3 |