| Главная Научный калькулятор | |
|
|
Задача №23Основание пирамиды - ромб, каждая боковая грань образует с плоскостью основания угол, равный 60°. Найдите площадь основания пирамиды, если высота пирамиды 9 см, а один из углов ромба 45°.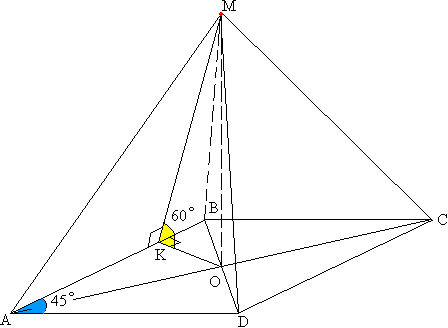 Построим двугранный угол между боковой гранью и основанием. Для этого в треугольнике АМВ проведем высоту МК. Теперь соединим точку К с точкой О (основанием высоты пирамиды). По теореме о трех перпендикулярах отрезок ОК перпендикулярен АВ. А угол МКО является линейным углом двугранного угла меджу основанием и боковой гранью и равен 60°. Из треугольника МКО: ОК=МОсtg∠МКО=3O3 Из треугольника АКО: АК=КОсtg∠ОАК=3O3 * сtg∠ОАК Известно, что диагонали ромба являются биссектрисами его углов и точкой пересечения делятся пополам (доказательство). Поэтому ∠ОАК=∠DАВ=45°/2=22,5° Из треугольника АВО: Знаем, что сумма острых углов в прямоугольном треугольнике равна 90 градусов ∠АВО=90°-∠ОАК=90°-22,5°=67,5° Из треугольника ОКВ: ∠ВОК=90°-∠АВО=90°-67,5°=22,5° КВ=КОtg∠ВОК=3O3 * tg∠ВОК АВ=АК+КВ=ОК(сtg∠ОАК+tg∠ВОК) Применим формулу тангенса половинного угла а затем связь тангенса и котангенса одинакового аргумента: 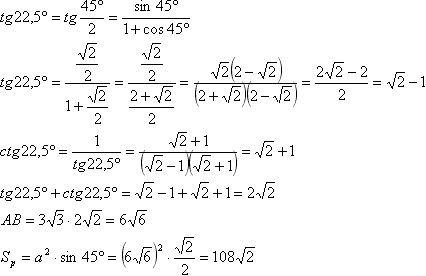
|