Задача №232

В равнобедренном треугольнике величина угла при основании равна 30 градусов. Длина высоты проведенной к основанию больше радиуса вписанной в треугольник окружности на 2 см. Найти длину основания этого треугольника.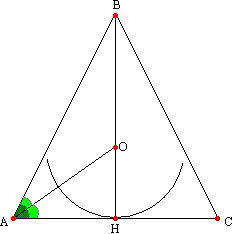
Обозначим основание высоты, проведенной к основанию треугольника за Н, а саму высоту за h.
В равнобедренном треугольнике углы при основании равны. Рассмотрим, например, угол ВАС. Вспомним свойство равнобедренного треугольника: высота равнобедренного треугольника, проведенная к основанию, является также биссектрисой и медианой. Значит (за одно и обозначим), АН=НС=х.
Как известно, центр вписанной окружности лежаит на пересечении биссектрис треугольника. Проведем еще одну биссектрису из вершины А для определения центра окружности. Обозначим его за Н, а отрезок ОН - радиус вписанной окружности, за r.
Продублируем данные: h-r=2, откуда h=2+r (1)
Из прямоугольных треугольников АВН и АОН соответственно найдем (с подстановкой выражения (1)):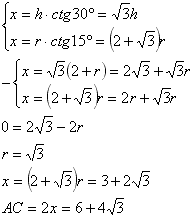