Задача №25

Стороны оснований правильной усеченной четырехугольной пирамиды равны 4 см и 6 см. Найдите площадь диагонального сечения, если боковое ребро образует с большим основанием угол, равный 45 градусов.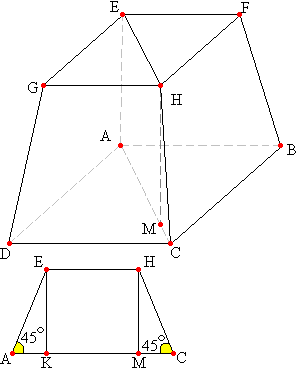
Раз пирамида правильная, то её диагональные сечения равны. Рассмотрим, например, сечение АЕНС. Т.к. пирамида правильная, боковые ребра её равны. Значит четырехугольник АЕНС является равнобедренной трапецией. Также из того, что пирамида правильная, следует, что плоские углы при основании равны. Из точки Н опустим перпендикуляр на плоскость АВСD. Используя теорему 9 темы трехгранный угол докажем, что этот перпендикуляр упадет на прямую АС. Знаем, что угол между прямой и плоскостью есть угол между этой прямой и её проекцией на эту плоскость. Т.е. угол между боковым ребром НС и основанием АВСD есть угол между НС и МС.
Вычертим сечение АЕНС.

ЕН = 4√2 (как диагональ в квадрате GEFH)

АС = 6√2 (как диагональ в квадрате АВСD)

Проведем высоту ЕК. Треугольники АЕК и МНС прямоугольные и равные по гипотенузе и острому углу, АК=МС. Четырехугольник КЕНМ является прямоугольником, т.к. в нем все углы прямые, поэтому ЕН=КМ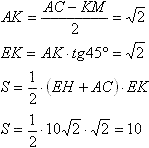