| Главная Научный калькулятор | |
|
|
Задача №27KABCD - правильная четырехугольная пирамида. Точки М и N - середины ребер KB и КС. Найдите периметр сечения пирамиды плоскостью, параллельной грани АКD и проходящей через точки М и N, если сторона основания пирамиды 16 см, а высота пирамиды 4 см.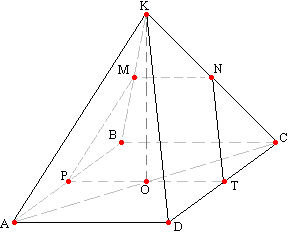 Итак, построим сечение. Соединим точки М и N. В треугольниках АКВ и СКD проведем прямые соответственно паралельно ребрам АК и DK. Вспомним теорему: параллельные линии отсекают на стронах угла пропорциональные отрезки. Поэтому точка Р и точка Т являются серединами соответственно ребер АВ и СD.
Отрезки MN, МР и NT являются пирамида правильная, то все боковые ребра равны, а высота падает центр основания. Произведем расчеты:
Итак, построим сечение. Соединим точки М и N. В треугольниках АКВ и СКD проведем прямые соответственно паралельно ребрам АК и DK. Вспомним теорему: параллельные линии отсекают на стронах угла пропорциональные отрезки. Поэтому точка Р и точка Т являются серединами соответственно ребер АВ и СD.
Отрезки MN, МР и NT являются пирамида правильная, то все боковые ребра равны, а высота падает центр основания. Произведем расчеты:1. Из треугольника АВС найдем АС по теореме Пифагора. 2. Найдем ОС как половину АС 3. Определим ребро КС из прямоугольного треугольника КОС по теореме Пифагора 4. Определим длины сторон сечения 5. Найдем периметр сечения, как сумму длин его сторон 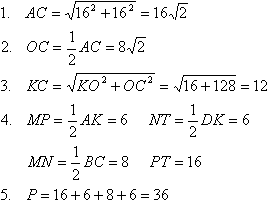
|