| Главная Научный калькулятор | |
|
|
Задача №31Основанием прямого параллелепипеда АВСDА1В1С1D1 является ромб АВСD, сторона которого равна а и угол равен 60 градусов. Плоскость АD1C1 составляет с плоскостью основания АВСD угол в 60°. Найти высоту ромба АВСD, высоту и площадь боковой поверхности параллелепипеда.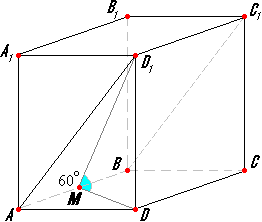 Ребра АС и C1D1 параллельны, т.к. перпендикулярны одной и той же грани АА1D1D. Параллельные линии определяют плоскость, причем тольку одну. Плоскость АВСD1 и плоскость АD1С1 имеют три общие точки, значит они совпадают, т.к. три точки определяют единственную плоскость. 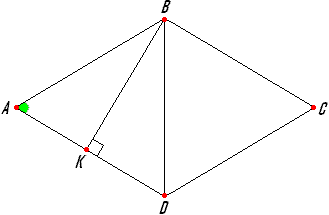 Проведем высоту ВК в ромбе АВСD и из треугольника АВК найдем её: ВК=АВ * sin60°=a * sin60° Также проведем высоту DM (высоты ромба равны). Теперь соединим точки М и D1. МD1 перпендикулярна ребру АВ по теореме о трех перпендикулярах. Таким образом, угол DМD1 является линейным углом двугранного угла между плоскостями АВСD и АВС1D1. Т.к. параллелепипед прямой, его боковые ребра является его высотами. Из прямоугольного треугольника DМD1 найдем DD1: DD1=DM * tg60°=a * sin60° * tg60°=3a/2 Площадь боковой поверхности прямого параллелепипеда находится как произведение его высоты и периметра основания: Sбок=P * h=4a * 3a/2=12a2/2 |