| Главная Научный калькулятор | |
|
|
Задача №57В трапеции АВСД: АД большее основание, угол Д равен 60 градусов, биссектриса угла С и угла Д пересекаются в точке О, ОД = а, ВС = b, АД = с.Найти площадь трапеции. 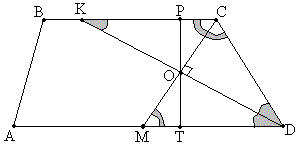 Так как СМ - биссектриса, углы ВСМ и МСD равны. Углы ВСМ и СМD равны как накрест лежащие для параллельных прямых ВС и AD и секущей СМ. Поэтому углы МСD и СМD равны. В треугольнике СМD два угла равны, а третий равен 60 градусов. Из этого получаем, что треугольник СМD равносторонний. Поэтому DO является и биссектрисой, и высотой, и медианой. Треугольники КСО и ОМD равны по стороне и прилищащим к ней углам: МО=ОС (DO - медиана), углы ВСМ и СМD равны (накрест лежащие для параллельных прямых ВС и AD и секущей СМ), углы КОС и МОD равны (вертикальные). Из равенства этих треугольников слудует равенство их соответствующих высот ОТ и ОР. Теперь рассмотрим треугольник ОDТ: катет противолежащий углу в 30 градусов равен половине гипотенузы. Или OT = 1/2OD = a/2. РТ = РО + ОТ = 2ОТ = а По имеющимся основаниям и высоте найдем площадь трапеции: |