| Главная Научный калькулятор | |
|
|
Задача №67Дана правильная шестиугольная призма со стороной основания а и большей диагональю b.Чему равен её объем. 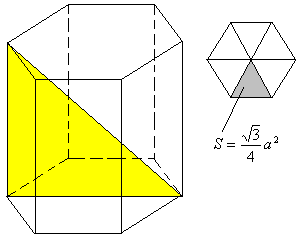 Определение. Правильной называется призма, в основании которой лежит правильный многоугольник, а перпендикуляр, проведенный через центр описанной около (или вписанной в) одного из оснований окружности, проходит и через центр окружности, описанной около (или вписанной в) другого основания. Другими словами это прямая призма, и все её боковые ребра перпендикулярны основаниям. Сначала найдем площадь основания: правильный шестиугольник состоит из шести правильных треугольника (как показано на риунке 1), поэтому можно просто умножить на 6 площадь правильного треугольника со стороной а: Теперь из прямоугольного треугольника, выделенного на рисунке желтым цветом, найдем высоту призмы, а затем и объем. Заметим, что здесь гипотенуза b и катет 2а: 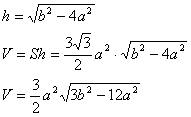
|