| Главная Научный калькулятор | |
|
|
Задача №85Прямая, параллельная основанию равнобедренного треугольника ABC, пересекает боковые стороны АВ и АС в точках M и N.Докажите, что треугольник AMN равнобедренный.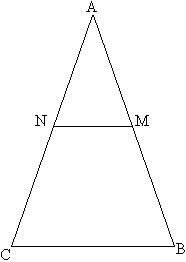 Теорема. В равнобедренном треугольнике углы при основании равны. Значит, ∠АВС = ∠АСВ Теорема. Внутренние односторонние углы при данных параллельных пямых и секущей в сумме составляют 180о. Т.е. ∠АВС + ∠NMB = 180о и ∠АСВ + ∠MNС = 180о, следовательно ∠MNС = ∠NMB Теорема. Сумма смежных углов равна 180о. Т.е. ∠АMN + ∠NMB = 180о и ∠ANM + ∠MNС = 180о, следовательно ∠АMN = ∠АNM Теорема.Если в треугольнике два угла равны, то такой треугольник равнобедренный (причем, сторона, к которой прилежат равные углы, есть основание, а две другие равны и называются боковыми). Значит, треугольник АМN равнобедренный. |