Задача №89

Вершина В ромба АВСD является центром окружности, радиус которой равен половине диагонали ВD. Докажите, что прямая АС является касательной к этой окружности.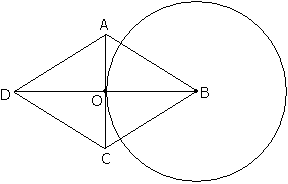

Теорема.Диагонали ромба пересекаются и точкой пересечения делятся пополам.
Из этой теоремы следует, что точка О лежит и на окружности, и на прямой АС.
Теорема. Диагонали ромба перпедикулярны между собой.
Из этой теоремы следует, что ОВ перпендикулярен АС.
Теорема. Если некоторая прямая имеет с окружностью общую точку такую, что радиус, проведенный в эту точку, образует с этой прямой угол 90^о, то эта прямая есть касательная к этой окружности.
Что и требовалось...