| Главная Научный калькулятор | |
|
|
Задача №99В основании пирамиды MABCD лежит ромб в котором AC=8, BD=6, высота(h)=1, все двугранные углы при основании равны, найдите S полной поверхности пирамиды.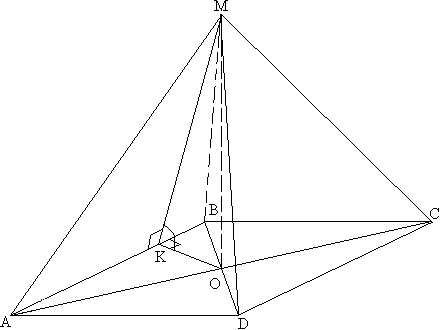 Теорема.Диагонали ромба пересекаются под прямым углом и точкой пересечения делятся попалам. Таким образом диагонали делят ромб на 4 равных прямоугольных треугольника с катетами 4 и 3. Гипотенуза есть сторона ромба, и она равна 5. Площадь основания равна сумме площадей четырех раных прямоугольных треугольника: Sосн=4*6=24 Из точки О опустим перпендикуляр на АВ. Теперь соединим точку К и вершиной пирамиды. МК перпендикулярна АВ по теореме о трех перпендикулярах ОК как высота в прямоугольном треугольнике есть отношение произведения катетов и гипотенузы: ОК=12/5 Из равенства всех двугранных углов при основании следует, что все апофемы подобные МК равны, а следовательно равны и площади всех боковых граней. Из прямоугольного треугольника МКО найдем гипотенузу по известным катетам: 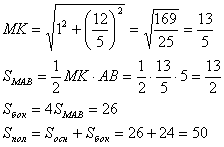
|