| Главная Научный калькулятор | |
|
|
Биссектриса треугольника
Определение 4. Любая из трех биссектрис внутренних углов треугольника называется биссектрисой треугольника.
Под биссектрисой угла треугольника также понимают отрезок между его вершиной и точкой пересечения биссектрисы с противолежащей стороной треугольника. Теорема 8. Три биссектрисы треугольника пересекаются в одной точке. 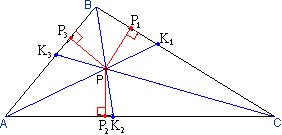 Действительно, рассмотрим сначала точку Р
пересечения двух биссектрис, например АК1 и ВК2. Эта
точка одинаково удалена от сторон АВ и АС, так как она лежит на биссектрисе
угла А, и одинаково удалена от сторон АВ и ВС, как принадлежащая биссектрисе
угла В. Значит, она одинаково удалена от сторон АС и ВС и тем самым принадлежит
третей биссектрисе СК3, то есть в точке Р
пересекаются все три биссектрисы.
Действительно, рассмотрим сначала точку Р
пересечения двух биссектрис, например АК1 и ВК2. Эта
точка одинаково удалена от сторон АВ и АС, так как она лежит на биссектрисе
угла А, и одинаково удалена от сторон АВ и ВС, как принадлежащая биссектрисе
угла В. Значит, она одинаково удалена от сторон АС и ВС и тем самым принадлежит
третей биссектрисе СК3, то есть в точке Р
пересекаются все три биссектрисы.Свойства биссектрис внутреннего и внешнего углов треугольника Теорема 9. Биссектриса внутреннего угла треугольника делит противолежащую сторону на части, пропорциональные прилежащим сторонам. 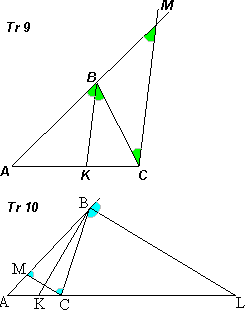 Доказательство. Рассмотрим треугольник АВС
и биссектрису его угла В. Проведем через вершину С прямую СМ, параллельную
биссектрисе ВК, до пересечения в точке М
продолжением стороны АВ. Так как ВК – биссектриса угла АВС, то ∠АВК=∠КВС.
Далее, ∠АВК=∠ВМС,
как соответственные углы при параллельных прямых, и ∠КВС=∠ВСМ,
как накрест лежащие углы при параллельных прямых. Отсюда ∠ВСМ=∠ВМС,
и поэтому треугольник ВМС – равнобедренный, откуда ВС=ВМ. По теореме о
параллельных прямых, пересекающих стороны угла, имеем АК:КС=АВ:ВМ=АВ:ВС,
что и требовалось доказать.
Доказательство. Рассмотрим треугольник АВС
и биссектрису его угла В. Проведем через вершину С прямую СМ, параллельную
биссектрисе ВК, до пересечения в точке М
продолжением стороны АВ. Так как ВК – биссектриса угла АВС, то ∠АВК=∠КВС.
Далее, ∠АВК=∠ВМС,
как соответственные углы при параллельных прямых, и ∠КВС=∠ВСМ,
как накрест лежащие углы при параллельных прямых. Отсюда ∠ВСМ=∠ВМС,
и поэтому треугольник ВМС – равнобедренный, откуда ВС=ВМ. По теореме о
параллельных прямых, пересекающих стороны угла, имеем АК:КС=АВ:ВМ=АВ:ВС,
что и требовалось доказать.Теорема 10 Биссектриса внешнего угла В треугольника АВС обладает аналогичным свойством: отрезки AL и CL от вершины А и С до точки L пересечения биссектрисы с продолжением стороны АС пропорциональны сторонам треугольника: Это свойство доказывается так же, как и предыдущее: на рисунке проведена вспомогательная прямая СМ, параллельная биссектрисе BL. Углы ВМС и ВСМ равны, а значит, и стороны ВМ и ВС треугольника ВМС равны. Из чего приходим к выводу AL:CL=AB:BC. 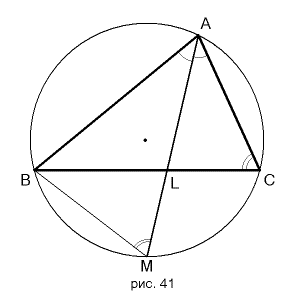 Теорема d4. (первая формула для биссектрисы): Если в
треугольнике ABC отрезок AL является биссектрисой угла A, то
Теорема d4. (первая формула для биссектрисы): Если в
треугольнике ABC отрезок AL является биссектрисой угла A, то
Теорема d5. (вторая формула для биссектрисы): В треугольнике
ABC со сторонами AB=a, AC=b и углом A, равным 2? и биссектрисой l, имеет
место равенство:
|