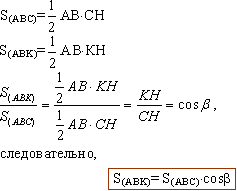Площадь ортогональной проекции плоской фигуры на плоскость
Теорема. Площадь ортогональной проекции плоской фигуры на плоскость есть
произведение площади самой фигуры на косинус угла между плоскостью фигуры и
плоскостью проекции.
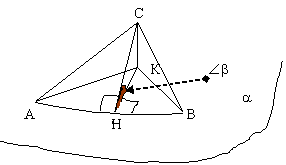
Доказательство. Докажем теорему на примере треугольника.
Пусть дана плоскость
a и треугольник АВС. Рассмотрим общий случай, когда
плоскость
a
и плоскость треугольника лежат под некоторым острым углом друг к другу. Для
упрощения решения плоскость
a проведем через одну из сторон треугольника, например
сторону АВ. Значит после проектирования точки А и В передут в себя, а точка С
переедет в точку К. В треугольнике АВС проведем высоту СН из вершины С. В
треугольнике АВК соединим точки К и Н. Прямая КН перпендикулярна прямой АВ (КН
– проекция прямой СН на плоскость
a, СН
^ АВ,
? КН
^ АВ по
теореме о трех перпендикулярах). Таким образом,
угол СНК – двугранный угол между плоскостями, обозначим его за
b.
Выразим площадь треугольников АВС и АВК и найдем их отношение:
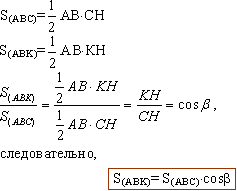
 Доказательство. Докажем теорему на примере треугольника.
Пусть дана плоскость a и треугольник АВС. Рассмотрим общий случай, когда
плоскость a
и плоскость треугольника лежат под некоторым острым углом друг к другу. Для
упрощения решения плоскость a проведем через одну из сторон треугольника, например
сторону АВ. Значит после проектирования точки А и В передут в себя, а точка С
переедет в точку К. В треугольнике АВС проведем высоту СН из вершины С. В
треугольнике АВК соединим точки К и Н. Прямая КН перпендикулярна прямой АВ (КН
– проекция прямой СН на плоскость a, СН ^ АВ,? КН ^ АВ по теореме о трех перпендикулярах). Таким образом,
угол СНК – двугранный угол между плоскостями, обозначим его за b.
Выразим площадь треугольников АВС и АВК и найдем их отношение:
Доказательство. Докажем теорему на примере треугольника.
Пусть дана плоскость a и треугольник АВС. Рассмотрим общий случай, когда
плоскость a
и плоскость треугольника лежат под некоторым острым углом друг к другу. Для
упрощения решения плоскость a проведем через одну из сторон треугольника, например
сторону АВ. Значит после проектирования точки А и В передут в себя, а точка С
переедет в точку К. В треугольнике АВС проведем высоту СН из вершины С. В
треугольнике АВК соединим точки К и Н. Прямая КН перпендикулярна прямой АВ (КН
– проекция прямой СН на плоскость a, СН ^ АВ,? КН ^ АВ по теореме о трех перпендикулярах). Таким образом,
угол СНК – двугранный угол между плоскостями, обозначим его за b.
Выразим площадь треугольников АВС и АВК и найдем их отношение: