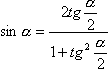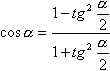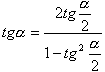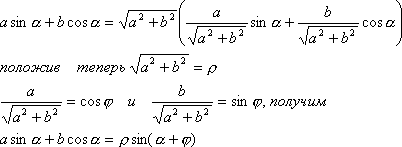Формулы тригонометрии

Тригонометрия :: Формулы

1	cos²α+sin²α=1
2
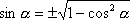
3
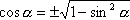
4
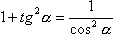
5
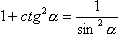
6	tgα⋅ctgα=1
7
8
9	cos2α=2cos²α-1
10	cos2α=1-sin²α

Формулы сложения и вычитания аргументов

11	sin(α + β) = sinαcosβ + cosαsinβ
12	sin(α – β) = sinαcosβ – cosαsinβ
13	cos(α – β) = cosαcosβ + sinαsinβ
14	cos(α + β) = cosαcosβ – sinαsinβ
15
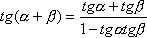
16
17
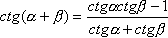
18

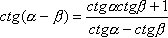
Формулы двойного аргумента

19	sin2α = 2sinαcosα
20	cos2α = cos²α – sin²α
21
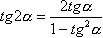
22

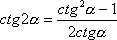
Формулы тройного аргумента

23	sin3α = 3sinα⋅cos²α – sin³α
24	sin3α = 3sinα – 4sin³α
25	cos3α = cos³α – 3cosα⋅sin²α
26	cos3α = 4cos³α – 3cosα
27
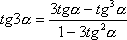
28

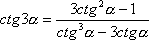
Формулы половинного аргумента

29
30
31
32
33
34

Формулы выражения основных тригонометрических функций через тангенс

35
36
37
38

Формулы преобразования произведения в сумму

39
40
41
42
43
44
45
46

Формулы преобразования сумм в произведение

47
48
49
50
51
52
53
54

Формула преобразования в произведение выражения a·sinα + b·cosα

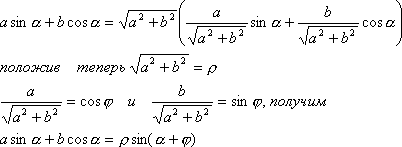
Формула преобразования в произведение выражений a·sinα + b, a·cosα + b, a·tgα + b, a·ctgα + b

56
57
58
59

Формулы для решения уравнений
60 sinx=α, x=(-1)ⁿarcsinα+πn, n∈Z (|a|≤1);
61 cosx=α, x=±arccosα+2πn, n∈Z (|a|≤1);
62 tgx=α, x=arctgα+πn, n∈Z (a∈R);
63 ctgx=α, x=arcctgα+πn, n∈Z (a∈R);

64 sinx=0, x=πn
65 sinx=1, x=π/2+2πn
66 sinx=-1, x=-π/2+2πn
67 cosx=0, x=π/2+πn
68 cosx=1, x=2πn
69 cosx=-1, x=π+2πn, где n∈Z