Сфера и шар. Площадь повержности, объём

Шаром называется тело, которое состоит из всех точек пространства, находящихся на расстоянии, не большем его радиуса, от данной точки - центра шара. Объём шара вычислим по формуле , для этого:
а. Найдем функцию, график которой мы будем вращать. Функция x² + y² = r² есть график окружности. Выразим y и получим: y = ±√r² - х², для простоты 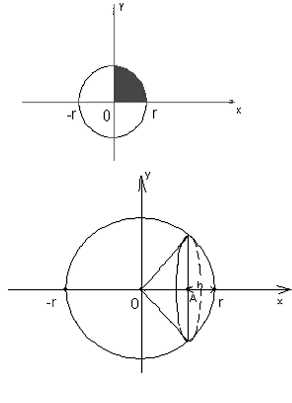возьмём положительную функцию у = √r² - х². Видно, что этот график симметричен относительно оси y, поэтому возьмём удвоенную правую часть: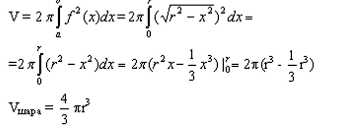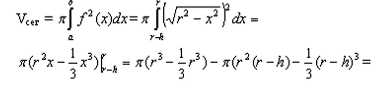

Шаровым сегментом называется часть шара, отсекаемая от него плоскостью. Вычислим объём сегмента шара. Обозначим центр круга, образовавшегося при пересечении шара плоскостью, через точку A а расстояние от точки А до сферы за h, тогда координата x у точки A будет равна r - h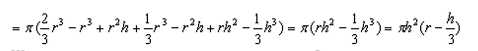

Шаровым сектором навывается тело, которое образуется из сегмента и конуса, вершина которого есть центр шара, а основание совпадает с основанием сегмента. Для нахождения объёма сектора нужно суммировать объёмы сектора и конуса. Объём сегмента известен . Найдем объём конуса:
Определимся: OA = r - h - высота конуса. Радиус основания конуса равен R = √r² - (r - h)² = √ - h² + 2rh. Площадь основания конуса равна . Объём конуса равен . Теперь складываем и получаем:

Шаровым слоем называется часть шара, заключенная между двумя параллельными плоскостями, пересекающими шар. Обозначим точки пересечения плоскостями оси Ox за A и B, и обозначим расстояние до этих точек от точки O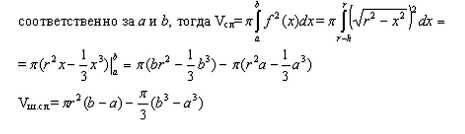