Неопределенный интеграл

Неопределенный интеграл. Раздел математики, изучающий свойства операции интегрирования и её приложения к решению задач физики и геометрии, называют интегральным исчислением.
Функцию F, заданную на некотором промежутке Х, называют первообразной для функции f, заданной на том же промежутке, если для всех х∈Х выполняется равенство F'(x)=f(x), или, что тоже самое dF(x)=f(x)dx.
Теорема. Если функция f имеет на промежутке Х первообразную F, то для любого числа С функция F+C также является первообразной для f. Иных первообразных функция f на Х не имеет.
Совокупность всех первообразных функции f называют неопределенным интегралом этой функции и обозначают символом ∫f(x)dx. Таким образом, ∫f(x)dx=F(x)+C, где F - одна из первообразных для f, а С пробегает множество действительных чисел. В этом равенстве f называют подынтегральной функцией, выражение f(x)dx - подынтегральным выражением, переменную х - переменной интегрирования и слагаемое С - постоянной интегрирования.
Свойства неопределенного интеграла:
а) Из определения первообразной вытекает: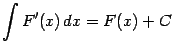

б) Из определения интеграла вытекает: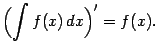

в) Интеграл от суммы функций равен сумме интегралов слагаемых: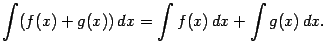

г) Постоянный множитель можно вынести за знак интеграла.

Непосредственное интегрирование

Непосредственное интегрирование основано на использовании результатов дифференцирования функции. Рассмотрим таблицу основных интегралов: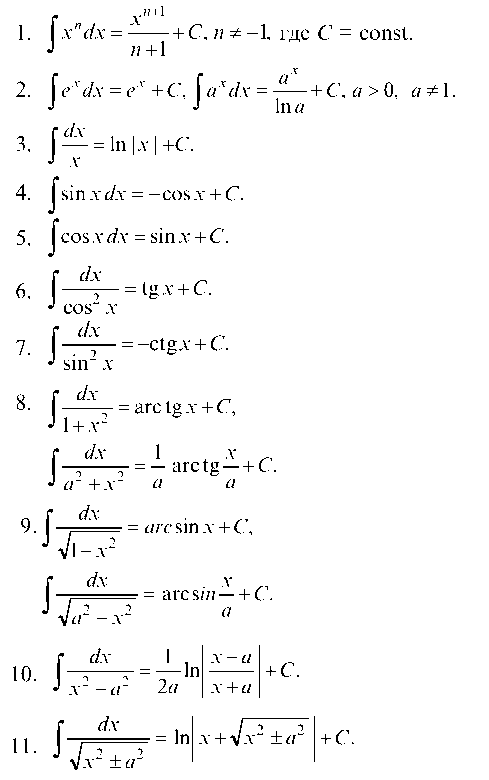

Замена переменной

Для интегрирования многих функций применяют метод замены переменной, или подстановки, позволяющий приводить интегралы к табличной форме.

Если функция f(z) непрерывна на [a, b], функция z =g (x) имеет на [a,b] непрерывную производную и α ≤ g(x) ≤ β, то

∫ f(g(x)) g^' (x) dx = ∫f(z) dz

причем после интегрирования в правой части следует сделать подстановку z=g(x).

Для доказательства достаточно записать исходный интеграл в виде:

∫ f(g(x)) g (x) dx = ∫ f(g(x)) dg(x).