| Главная Научный калькулятор | |
|
|
Равенство треугольниковТеорема 13. Если в двух (и более) данных треугольниках соответственно равны одна сторона и прилегающие к ней углы, то такие треугольники равны.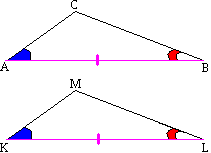 Пусть в двух треугольниках АВС и КLМ стороны АВ и KL
и прилежащие к ним углы А, К и В, L соответственно равны. Докажем, что треугольники равны.
Пусть в двух треугольниках АВС и КLМ стороны АВ и KL
и прилежащие к ним углы А, К и В, L соответственно равны. Докажем, что треугольники равны.Действительно, наложим треугольник АВС на треугольник КLМ, чтобы сторона АВ совпала со стороной КL, а сторона АС пошла по стороне КМ, что возможно в силу равенства углов А и К. Тогда и сторона ВС пойдет по стороне LМ тем самым совпадут вершины С и М, как точки пересечения совпадающих сторон. Ясно, что в условии можно предположить равенство другой пары соответствующих углов, так как из равенства двух пар углов следует и равенство третей пары углов треугольников. Теорема 14. Если две стороны и угол заключенный между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. 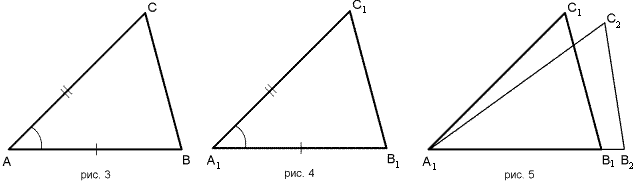 Доказательство: Пусть у треугольников ABC и A1B1C1 угол A равен углу A1, AB = A1B1, AC = A1C1 (рис. 3, 4). Докажем, что треугольники равны. Пусть A1B2C2- треугольник, равный треугольнику ABC, с вершиной B2 на луче A1B1 и вершиной C2 в той же полуплоскости относительно прямой A1B1, где лежит вершина C1 (рис. 5). Этот треугольник существует по VIII аксиоме. Так как A1B1 = A1B2, то по аксиоме об откладывании отрезков (аксиома VI) вершина B1 совпадает с вершиной B2 (рис. 6). Так как угол B1A1C1 равен углу B2A1C2, то по аксиоме об откладывании углов (аксиома VII) луч A1C1 совпадает с лучом A1C2 (рис. 7). Но так как A1C1 = A1C2, по VI аксиоме вершина C1 совпадает с вершиной C2 (рис. 8). Значит, треугольник A1B1C1 равен треугольнику A1B2C2, который равен треугольнику ABC. Что и требовалось доказать. 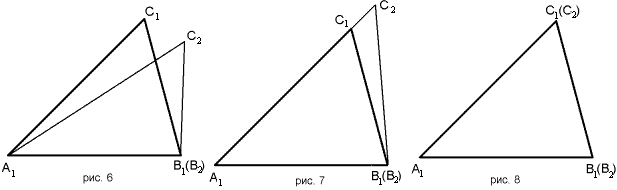 Теорема 15. Если три стороны одного треугольника соответственно равны трем сторонам другого, то треугольники равны. 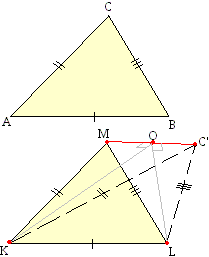 Для доказательства наложим сторону АВ треугольника АВС на
сторону KL так, чтобы
совпали точки А и К, В и L,
а вершины С и М оказались по одну сторону от совмещенных сторон. Остается
показать, что и вершины С и М совпадут. Допустим противное, а именно что С и М
не совместились. Пусть точка О – середина отрезка между этими вершинами. Тогда,
в силу равенства наклонных КМ и КС’ к прямой МС’, отрезок КО будет
перпендикуляром к МС’. Также должен быть перпендикуляром к МС’ и отрезок LO, т.е. в точке О мы имеем
два перпендикуляра к МС’, что невозможно. Итак, допущение что М и С’ не
совпадают, ложно.
Для доказательства наложим сторону АВ треугольника АВС на
сторону KL так, чтобы
совпали точки А и К, В и L,
а вершины С и М оказались по одну сторону от совмещенных сторон. Остается
показать, что и вершины С и М совпадут. Допустим противное, а именно что С и М
не совместились. Пусть точка О – середина отрезка между этими вершинами. Тогда,
в силу равенства наклонных КМ и КС’ к прямой МС’, отрезок КО будет
перпендикуляром к МС’. Также должен быть перпендикуляром к МС’ и отрезок LO, т.е. в точке О мы имеем
два перпендикуляра к МС’, что невозможно. Итак, допущение что М и С’ не
совпадают, ложно.Для двух прямоугольных треугольников достаточно допустить равенство двух пар сторон: Теорема 16. Два прямоугольных треугольника равны, если два катета одного равны двум катетам другого или если катет и гипотенуза одного равны соответственно катету и гипотенузе другого. Так как у двух прямоугольных треугольников всегда есть пара равных углов (прямых), то для равенства таких треугольников достаточны также следующие условия: Теорема 17. Прямоугольные треугольники равны, если они имеют пару равных острых углов и пару равных катетов (или гипотенуз). |