Средняя линия треугольника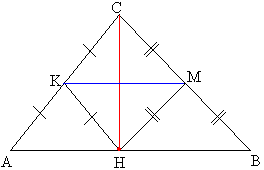

Определение 13. Средней линией треугольника называют отрезок, соединяющий середины двух сторон треугольника.
Каждый треугольник имеет три средних линии.
Теорема 43. Каждая из средних линий треугольника, соединяющих середины двух данных сторон, параллельна третей стороне и равна её половине.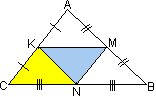

Рассмотрим треугольник АВС. Опустим высоту СН на сторону АВ. Она разобьёт треугольник на два прямоугольных треугольника АСН и СВН. Проведем медианы НК и НМ соответственно в этих треугольниках По свойству медианы прямоугольного треугольника, проведенной из вершины Н прямого угла, найдем НК=СК и также НМ=СМ. Теперь точки К и М, как равноудаленные от точек Н и С, лежат на перпендикуляре, проведенном к высоте в её середине, а потому отрезок, соединяющий их, параллелен стороне АВ треугольника. Теперь следует рассмотреть треугольник, в котором проведены все три средние линии. Для примера: четырехугольник АКМN является параллелограммом по определению (противоположные стороны параллельны по доказанному ранее). А в параллелограмме противоположные стороны равны, поэтому КМ=СN=1/2CB. Проведем подобные доказательства и получим, KN=1/2AB и MN=1/2AC