Стороны и углы треугольника.

Длины сторон треугольника (короче, стороны треугольника) не могут быть заданы произвольно. Действительно, для произвольного треугольника АВС сумма двух любых сторон больше третей стороны: АВ + ВС > АС, так как ломаная длиннее отрезка прямой. Из этого же неравенства находим АС – АВ < ВС, то есть разность двух любых сторон треугольника меньше его третей стороны. Например, из отрезков а = 5, b = 8, с = 14 нельзя построить треугольник, так как 14>5+8. Если же даны три отрезка a,b,c такие, что больший из них меньше суммы двух других, то можно построить треугольник, то можно построить треугольник, имеющий данные отрезки своими сторонами. Итак,
Теорема 1. Сумма длин двух любых сторон треугольника больше длины третьей стороны этого треугольника. (a + b > c, где с – наибольший из трех отрезков).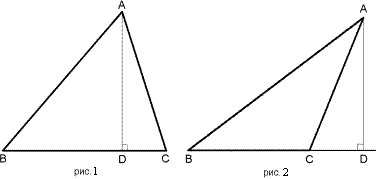
Доказательство: Пусть ABC - данный треугольник. Докажем, что AB + AC > BC. Опустим из вершины A этого треугольника высоту AD. Рассмотрим два случая:
1) Точка D принадлежит отрезку BC, или совпадает с его концами (рис.1). В этом случае AB>DB и AC>DC, так как длина наклонной больше длины проекции наклонной. Сложив эти два неравенства, получим, что AB + AC > BD + DC = BC. Что и требовалось доказать.
2) Точка D не принадлежит отрезку BC (рис.2). В этом случае BD<BA, так как наклонная больше проекции наклонной, а следовательно, BC < BD < BA < BA + AC. Что и требовалось доказать.
Для остальных пар сторон неравенство треугольника доказывается аналогично. Теорема доказана полностью.
Теорема 2. Сумма углов любого треугольника равна 180 градусов.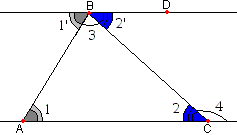
Доказательство. Рассмотрим произвольный треугольник АВС и проведем через одну из его вершин, например В, прямую BD, параллельную противоположной стороне АС. Теперь из чертежа ясно, что ∠1’ = ∠1 и ∠2’ = ∠2 (накрест лежащие углы), и так как 1’ + 2’ + 3 = 180°, то 1 + 2 + 3 = 180°, что и требовалось доказать.

Продолжая сторону АС, находим как следствие:

Теорема 3. Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
Теорема 3.1 Тем самым, внешний угол треугольника больше каждого из его внутренних углов, с ним не смежных.
Действительно, на рисунке ∠4=180°-∠2 (как смежные)
Также ∠2=180°-(∠1+∠3)
Подставляя второе выражение в первое, получаем: ∠4=∠1+∠3
Ну, а так как ни один из углов не может равняться нулю, каждый из этих углов меньше внешнего, например, ∠1=∠4-∠3 или ∠1<∠4
Таким образом, зная два угла треугольника, можно найти и третий. Ясно также, что если один угол в треугольнике прямой или тупой, то два других его угла острые.
Определение 1. Если один угол треугольника тупой, то треугольник называется тупоугольным.
Определение 2. Если один угол треугольника прямой, то треугольник называется прямоугольным.
Определение 3. Если все три угла треугольника острые, то треугольник называется остроугольным.
Из задач на построение треугольников видно, что при любых данных положительных углах α, β, γ, составляющих в сумме два прямых, существуют треугольники, имеющие α, β, γ своими внутренними углами. Итак,
Теорема 4.Условие a + b + g = 180° необходимо и достаточно для существования треугольника с углами a, b, g. Так как внешний угол треугольника дополняет внутренний смежный с ним угол до развернутого угла, то
Теорема 5. Сумма внешних углов треугольника равна 360°.
Связь между величинами сторон и углов треугольника устанавливает следующая
Теорема 6. Против большей стороны в треугольнике лежит больший угол.
Теорема 6.1. Против равных сторон лежат равные углы.
Теорема 7. В любом треугольнике против большего угла лежит большая сторона.
Теорема 7.1. Против равных углов лежат равные стороны.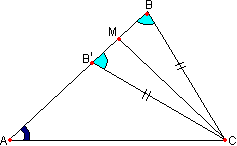
Доказательство. Применим свойство наклонных. Пусть в треугольнике АВС сторона АС больше стороны ВС. Проведем высоту СМ треугольника. Так как наклонная СВ меньше наклонной СА, то её основание В лежит ближе к основанию высоты СМ, чем основание А наклонной СА. Поэтому, если перегнуть рисунок по СМ, то угол при вершине В перейдет во внешний угол B’ треугольника АСB’ и, следовательно, будет больше угла А, как внутреннего с ним не смежного. Итак, если между сторонами треугольника имеются неравентсва a < b < c, то соответственно и противолежащие углы удовлетворяют неравенствам a < b < g. Равенство углов, лежащих против равных сторон, сразу получится, если учесть, что равные наклонные расположены относительно перпендикуляра симметрично и совмещаются при сгибе плоскости по перпендикуляру. При этом совмещаются и углы, равенство которых должно быть доказано.
Обратное утверждение, говорящее, что против большего угла лежит большая сторона, получается рассуждением от противного. Так, пусть a < b. Если бы мы имели a > b или a = b, то должно было бы быть a > b или a = b, что противоречит условию. Поэтому a < b, что и требовалось доказать. Так же доказывается, что против равных углов расположены равные стороны. В частности, равносторонний треугольник является и равноугольным. Каждый из его углов в этом случае равен 60°