Задача №100

Найти площадь круга, если стороны вписанного в него прямоугольника равны 8 см и 16 см.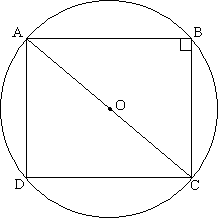
Теорема.Если на хорду опирается прямой угол, вершина которого лежит на окружности, то такая хорда является диаметром.
Таким образом, АС есть диаметр данной окружности. Определим его по теореме Пифагора из треугольника АВС:
АС²=АВ²+ВС²
АС²=16²+8²
АС²=320
Площадь круга определим по формуле:
S=πd²/4 = 80π