| Главная Научный калькулятор | |
|
|
Задача №108Сторона основания правильной четырехугольной пирамиды равна 3 см, а каждая боковая грань наклонена к плоскости основания под углом 60 градусов. Найти объем вписанного в эту пирамиду шара.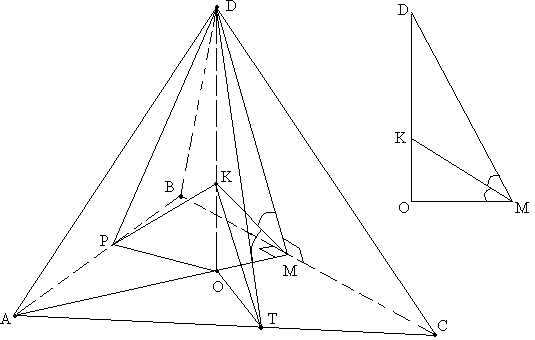 Определим положение линейного угла между бок гранью и основанием. Для этого из точки О опустим перпендикуляр на ВС (точку пересечения обозначим за М). Теперь соединяем точки D и М. DМ перпендикулярна ВС (по теореме о трех перпендикулярах). Значит угол DМО – линейный угол двугранного угла между гранями DВС и АВС. Надо заметить, что ОМ является частью отрезка АМ (т.к. тругольник АВС правильный). Также АМ является как высотой, так и медианой. Из прямоугольного треугольника АМС определим сторону АМ по теореме Пифагора, а затем ОМ как третью часть (свойство медиан треугольника) от АМ: 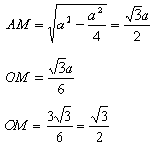 Как известно центр вписанного в пирамиду шара лежит в точке пересечения биссекторных плоскостей двугранных углов между гранями пирамиды. Для правильной пирамиды определение несколько легче: центр вписанного в правильную пирамиду шара лежит в точке пересечения биссектрисс линейных углов двугранных углов между боковыми гранями и основанием построенных на соответственных апофемах и высотах основания. Все эти биссектрисы пересекутся в одной точке (К), которая лежит на высоте пирамиды. Это следует из равенства прямоугольных треугольников DOM, DOP, DOT по катету (DО общая) и острому углу (все грани наклонены к основанию под одинаковым углом). Радиусом будет расстояние от этой точки до одной из граней пирамиды. У нас уже есть ОК, его и найдем. В треугольнике КОМ угол КМО равен 30 градусов - половина угла DМО. 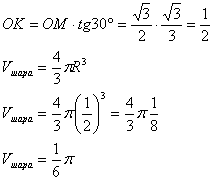
|