| Главная Научный калькулятор | |
|
|
Задача №126Около шара описан усеченный конус, площадь осевого сечения которого S, а острый угол сечения альфа. Найти объём шара.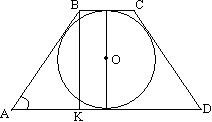 Рассмотрим осевое сечение: Осевым сечением конуса является равнобокая трапеция. Обозначим её высоту за h. Из прямоугольного треугольника АВК АВ=h/sinα. Теорема. Если в трапецию можно вписать окружность, то сумма длин её боковых сторон равна сумме длин оснований. Т.е. ВС+AD=AB+CD=2AB (т.к. трапеция равнобокая) ВС+AD=2АВ=2h/sinα. Запишем формулу площади трапеции: S=1/2(a+b)h=h2/sinα, откуда h2=Ssinα Заметим, что высота равна диаметру вписанной окружности: 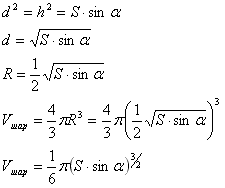
|