| Главная Научный калькулятор | |
|
|
Задача №140Через точку А окружности проведенны диаметр АС и две хорды АВ и АD, равные радиусу. Найдите углы четырехугольника АВСD и градусные меры дуг АВ, ВС, СД, АД.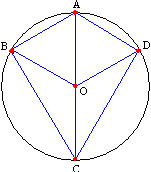 Треугольники АВО и АDО равносторонние (все стороны равны радиусу), поэтому все их углы равны 60 градусов. ∠ВАD=∠ВАО+∠ОАD=120о.
Треугольники АВО и АDО равносторонние (все стороны равны радиусу), поэтому все их углы равны 60 градусов. ∠ВАD=∠ВАО+∠ОАD=120о.Пользуясь тем, что сумма противолежащих углов выписанного в окружность четырехугольника равна 180 градусов, запишем: ∠ВСD=180о-∠ВАD=60о. Известно, что если вписанный угол опирается на диаметр, то он равен 90 градусов, поэтому углы В и D четырехугольника АВСD равны 90 градусов. Напомню, что градусная мера дуги - это величина центрального угла, опирающегося на эту дугу. Для АВ ∠АОВ=60о. Для ВС ∠СОВ как смежный для ∠АОВ равен 120о. Для АD ∠АОD=60о. Для СD угол САD, как смежный для угла АОD, равен 120 грдусов. |