| Главная Научный калькулятор | |
|
|
Задача №145Треугольник ABC вписан в окружность с центром O и радиусом 4. Найти площадь треугольника BOC, если угол B=40 градусов, а угол C=35 градусов.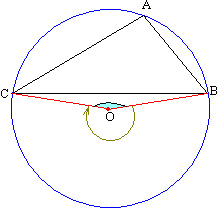 Зная теорему о сумме углов треугольника, запишем:
Зная теорему о сумме углов треугольника, запишем:∠А+∠В+∠С=180о, откуда ∠А=180о-∠В-∠С=180о-40о-35о=105о По теореме: вписанный угол равен половине центрального угла, опирающегося на ту же дугу, ∠ВОС=2∠А=210о Угол, который мы только что нашли, обозначен на рисунке стрелкой, нам нужен не он, а противоположный, т.е: 360о-210о=150о SBOC=1/2*OB*OC*sin150o=4 |