| Главная Научный калькулятор | |
|
|
Задача №150Доказать, что сумма расстояний от любой точки внутри правильного пятиугольника ABCDE до прямых AB, BC, CD, DE и EA одна и та же.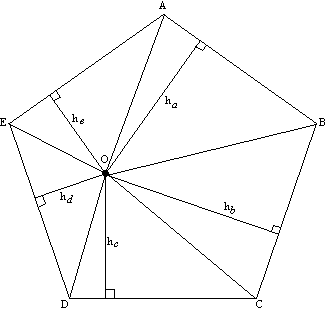 Возьмем, например, такую точку О. Обозначим расстояния от неё до соответственных сторон за ha, hb, hc, hd и he.
Возьмем, например, такую точку О. Обозначим расстояния от неё до соответственных сторон за ha, hb, hc, hd и he.Соединим точку О с вершинами пятиугольника. Образовалось пять треугольников. Сумма площадей этих треугольников постоянна и равна площади самого пятиугольника. Найдем площадь каждого треугольника по отдельности, а затем сложим 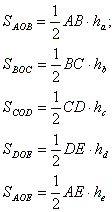 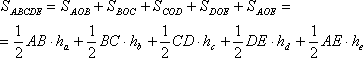 Стороны фигуры равны, поэтому, обозначая их за а, получаем: 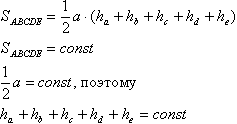 Иными словами, как площадь, так и длина стороны (половины стороны) пятиугольника постоянны, поэтому и сумма, заключенная в скобках, должна быть постоянной для выполнения равенства const=const Произведение постоянных является постоянным числом const'*const"=const Произведение постоянного и непостоянного и двух непостоянных чисчел не является постоянным числом! |