| Главная Научный калькулятор | |
|
|
Задача №158В равнобедренной трапеции ABCD (AB=CD):1. Одно из оснований равно 8 см, а другое - 14 см. Один из углов равен 120 градусов. Найти АВ и CD. 2. Пусть СЕ - высота. Доказать, что АЕ=(AD+ВC)/2. 3. tg∠CAD=5/6, а высота равна 60. Найти площадь трапеции. 4. высота, проведенная из вершины тупого угла делит среднюю линию на отрезки 2 см и 6 см. Найти основание трапеции. 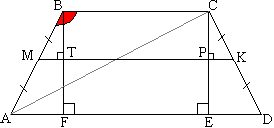 1. Проведем высоты трапеции ВF и CE.
1. Проведем высоты трапеции ВF и CE. По свойству 1 равнобокой трапеции ∠АВС=∠ВСD=120° Сумма односторонних углов равна 180°, поэтому ∠BAD=180°-∠АВС=60° Также по свойству 1 равнобокой трапеции ∠BAD=∠CDA=60°. В четырехугольнике ВСЕF все углы прямые по построению, поэтому он является прямоугольником по признаку 3. Вспомним такое свойство: Противолежащие стороны прямоугольника равны. Поэтому ВС=EF. Треугольники АВF и DCE - прямоугольные по построению и равны по острому углу и гипотенузе (∠BAD=∠CDA=60° и АВ=CD - боковые стороны). Поэтому равны и их катеты AF=DE. AF+DE=AF+AF=2AF=AD-EF=AD-BC AF=(AD-BC)/2=(14-8)/2=3. Из прямоугольного треугольника АВF: АВ=АF/cos60°=6 AB=CD=6 2. AE=AF+FE=AF+BC=(AD-BC)/2+BC=AD/2-BC/2+BC=(AD+BC)/2 ч.т.д. 3. Из прямоугольного треугольника АСЕ: tg∠CAD=СЕ:АЕ=5/6, (СЕ - высота, СЕ=60) откуда: АЕ=6/5СЕ=72 Из пункта 2. известно: AE=(AD+BC)/2=72 Найдем площадь трапеции: S=CE*(AD+BC)/2=60*72=4320 4. МТ=2 и ТК=6 - условие. Рассмотрим высоту BF. Она перпендикулярна средней линии МК (если прямая перпедикулярна одной из параллельных прямых, то она перпендикулярна и второй). Прямоугольные треугольники АВF и МВТ подобны по острому углу (∠МВТ - общий), поэтому: МТ:AF=МВ:АВ, где МВ=1/2АВ по условию, поэтому AF=2МТ=4 AF=ЕD=4 В четырехугольнике ВСРТ все углы прямые по построению, поэтому он является прямоугольником по признаку 3. Вспомним такое свойство: Противолежащие стороны прямоугольника равны. Поэтому ВТ=СР. Прямоугольные треугольники МВТ и КСР равны по катету и гипотенузе (ВТ=СР и МВ=КС, как половины боковых сторон), поэтому МТ=РК=2 и ТР=ТК-РК=6-2=4 ВС=ТР=FE=4 AD=AF+FE+ED=12 |