| Главная Научный калькулятор | |
|
|
Задача №160В трапеции ABCD AD=16 BC=9. На продолжение стороны BC взята точка M так что CM=3,2. В каком соотношение прямая AM делит площадь ABCD?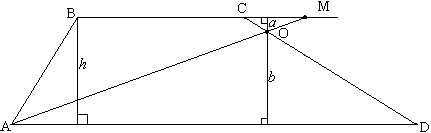 Обозначим точку пересечения АМ и СD за О. Обозначим высоту трапеции (расстояние между параллельными прямыми ВС и AD) за h. Через точку О проведем высоту, а части, на которые она её разбывает, обозначим за а и b, как показано на рисунке.
Обозначим точку пересечения АМ и СD за О. Обозначим высоту трапеции (расстояние между параллельными прямыми ВС и AD) за h. Через точку О проведем высоту, а части, на которые она её разбывает, обозначим за а и b, как показано на рисунке.Треугольники АОВ и СОМ подобны по двум углам (∠АОВ=∠СОМ - вертикальные; ∠МСО=∠ODA - внутренние накрест-лежащие), поэтому: a:b=CM:AD a:b=3,2:16=0,2 a=0,2b h=a+b=1,2b b=5/6 * h SAOD=1/2 * b * AD=8 * 5/6 * h=20/3 * h SABCD=1/2(AD+BC) * h=25/2 * h SABCO=SABCD-SAOD SABCO=25/2 * h-20/3 * h=35/6 * h SABCO:SAOD=35/6 * h:20/3 * h=7:8 |