| Главная Научный калькулятор | |
|
|
Задача №163Через сторону нижнего основания правильной треугольной призмы проведена плоскость, пересекающая боковые грани по отрезкам,угол между которыми α. Найдите угол наклона этой плоскости к основанию призмы. 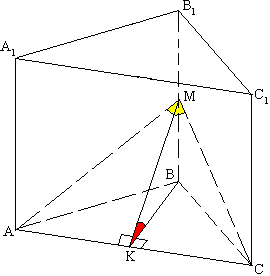 Прямоугольные треугольники АМВ и СМВ равны по двум катетам (МВ - общая, АВ=ВС - стороны правильного треугольника АВС). Поэтому АМ=СМ, т.е. треугольник АМС равнобедренный. По теореме 2:
Прямоугольные треугольники АМВ и СМВ равны по двум катетам (МВ - общая, АВ=ВС - стороны правильного треугольника АВС). Поэтому АМ=СМ, т.е. треугольник АМС равнобедренный. По теореме 2:∠МАС=∠МСА=(180°-α)/2=90°-α/2 Из точки М опустим перпендикуляр МК на АС. Соединим К и В. ВК перпендикулярна АС по теореме о трех перпендикулярах. Угол МКВ - искомый. Применим формулу связи косинусов: cos∠МАС=cos∠МАВ * cos∠ВАС cos∠(90°-α/2)=cos∠МАВ * cos60° cos∠МАВ=2sinα/2 Применим формулу связи синусов: sin∠МАВ=sin∠МАC * sin∠MKB 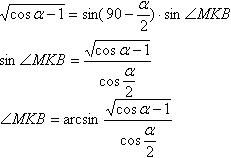
|