| Главная Научный калькулятор | |
|
|
Задача №165Найдите высоту правильной шестиугольной призмы, если сторона её основания равна а, а меньшая из диагоналей призмы равна b. 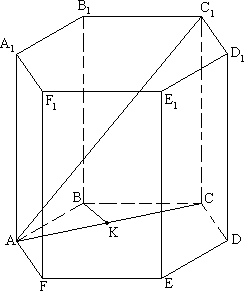 Сначала найдем меньшую диагональ. Возьмем диагональ АС1. Она меньшая. Для доказательства этого сравним прямоугольные треугольники АСС1 и АDD1. Катеты СС1 и DD1 у них равны, а вот AD>АС, поэтому и гипотенуза AD1 больше, чем АС1.
Сначала найдем меньшую диагональ. Возьмем диагональ АС1. Она меньшая. Для доказательства этого сравним прямоугольные треугольники АСС1 и АDD1. Катеты СС1 и DD1 у них равны, а вот AD>АС, поэтому и гипотенуза AD1 больше, чем АС1.Рассмотрим треугольник АВС. Он равнобедренный (АВ=ВС по условию). Опустим перпендикуляр ВК на АС. По свойству равнобедренного треугольника ВК является также и медианой, и биссектрисой. Поэтому АК=КС. Каждый из углов правильного шестиугольника равен 120 градусов, значит, ∠АВК=∠СВК=60°. В прямоугольном треугольнике АВК: 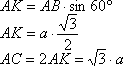 Из прямоугольного треугольника АСС1: |