| Главная Научный калькулятор | |
|
|
Задача №198Сторона квадрата ABCD равна 2. Найти радиус окружности, которая касается: стороны AB, диагонали AC и окружности, описанной около ABCD. 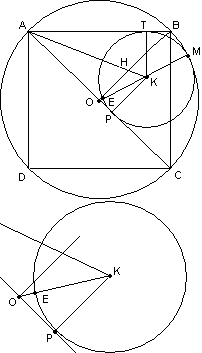 Теорема. Центры и точка касания внутрекасающихся и внешнекасающихся окружностей лежат на одной прямой. Пользуясь этой теоремой, проведем прямую ОМ.
Теорема. Центры и точка касания внутрекасающихся и внешнекасающихся окружностей лежат на одной прямой. Пользуясь этой теоремой, проведем прямую ОМ.Для касательной ОС и секущей ОМ запишем теорему 10 темы круг и окружность, которая гласит: Если из точки к окружности проведены касательная и секущая, то квадрат отрезка касательной от данной точки до точки касания равен произведению длин отрезков секущей от данной точки до точек её пересечения с окружностью 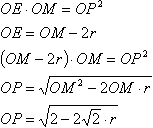 Т.к. центр описанной около квадрата окружности лежит на пересечении его диагоналей, в котором они делятся пополам, то соединив точки В и О, мы получим медиану треугольника АВС. По свойству равнобедренного треугольника эта медиана является также высотой и биссектрисой. Точка К равноудалена от АВ и АС (КТ=КР), поэтому АК является биссектрисой угла САВ. Биссектрисы АК и ВО пересекаются в точке Н. Точка пересечения биссектрис треугольника - центр вписанной в этот треугольник окружности. Значит ОН - радиус окружности вписанной в треугольник АВС. Найдем его: Прямоугольные треугольники АКР и АНО подобны по острому углу, поэтому: 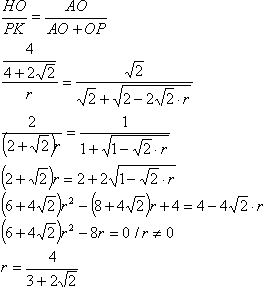
|