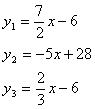Задача №2

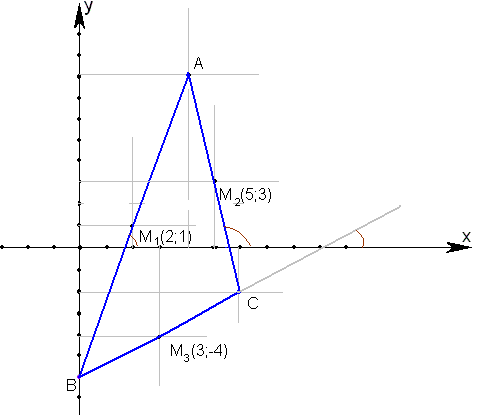
Даны середины сторон треугольника: М₁ (2;1), М₂ (5,3) и М₃ (3;-4). Составить уравнение его сторон. Пусть вершины данного треугольника точки А (х;у) В( х₁;у₁) и С(х₂;у₂)

Как известно общий вид уравнения прямой в плоскости –  у = kx + b

Из этого уравнения следует, что для того, чтобы найти уравнение прямых содержащих стороны, необходимо знать:

Коэффициент k равный тангенсу угла между прямой и положительным направлением оси Ох

Число b – свободный член или координата у в тот момент, когда прямая пересекает ось Оу

Для нахождения этих параметров определим координаты вершин треугольника:

Пусть точка М₁ – середина стороны АВ, М₂ – АС и М₃ – ВС, тогда по формуле середины отрезка составляем уравнения

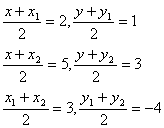
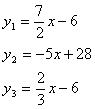
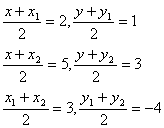откуда определяем координаты вершин А (4;8) В( 0;-6) и С(6;-2)

Соединим вершины и выделим углы, тангенсы которых нам необходимо найти.

Введем  следующие обозначения:

Прямая, содержащая сторону 1) АВ – у₁ =k₁x + b₁

2) АC – у₂ =k₂x + b₂

3) CВ – у₃ =k₃x + b₃

Составим два уравнения соответственно  для точек А и точки В

 8 = 4k₁ + b₁

-6 = 0k₁ + b₁, откуда k₁ = 7/2      и b₁ = -6

Составим два уравнения соответственно  для точек А и точки C

8 = 4k₁ + b₁

-2 = 6k₁ + b₁, откуда k₁ = -5      и b₁ = 28

Составим два уравнения соответственно  для точек C и точки В

-2 = 6k₁ + b₁,

-6 = 0k₁ + b₁, откуда k₁ = 2/3      и b₁ = -6

Ответ: