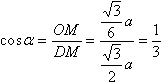Задача №20

Все рёбра правильной треугольной пирамиды равны между собой. Найдите косинус угла между боковой гранью и плоскостью основания.

Для начала определим пирамиду пусть это будет пирамида АВСD с основанием АВС и вершиной D.

Все ребра равны, значит, все грани правильные треугольники. Обозначим ребро за а.

Т.к. это правильная пирамида, то высота, проведенная из вершины на основание, падает в центр основания и все двугранные углы между боковыми гранями и основанием равны. Возьмем ВСD.

Для нахождения косинуса двугранного угла между этой гранью и основанием определим положение линейного угла. Для этого из точки О опустим перпендикуляр на ВС (точку пересечения обозначим за М). Теперь соединяем точки D и М. DМ перпендикулярна ВС (по теореме о трех перпендикулярах).

Значит угол DМО – линейный угол двугранного угла между гранями DВС и АВС.

Надо заметить, что ОМ является частью отрезка АМ (т.к. тругольник АВС правильный). Также АМ является как высотой, так и медианой.

Из прямоугольного треугольника АМС определим сторону АМ по об этом подробнее здесь):

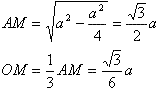
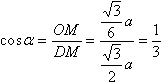
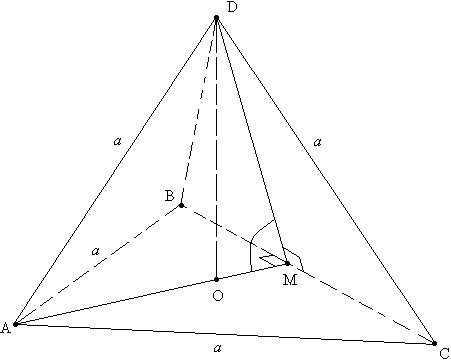
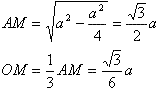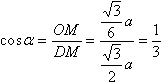
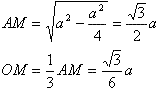Надо заметить, что DМ = АМ (высоты в равных треугольниках ), поэтому: