| Главная Научный калькулятор | |
|
|
Задача №202Длина основания равнобедренного треугольника вписанного в окружность равна а, а высота, проведенная к основанию, - b. Найти диаметр окружности. 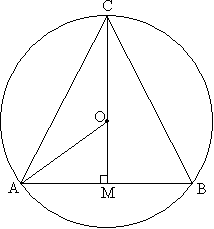 Пользуять свойством равнобедренного треугольника заключаем, что высота СМ является также и серединным перпендикуляром основания (АМ=МВ=a/2).
Пользуять свойством равнобедренного треугольника заключаем, что высота СМ является также и серединным перпендикуляром основания (АМ=МВ=a/2).Теорема. Центр описанной около треугольника окружности лежит на пересечении серединных перпендикуляров к сторонам треугольника (доказательство). Из этих теорем вытекает следующее: точка О - центр окружности лежит на высоте СМ. Проведем радиус АО и обозначим радиус окружности за R: АО=СО=R. СМ=СО+ОМ=R+OM, откуда ОМ=СМ-R=b-R Запишем теорему Пифагора в треугольнике АОМ: 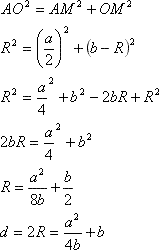
|