Задача №203

Стороны треугольника ABC разделены точками MNP так, что AM:MB=BN:NC=CP:PA=1:4. Q - точка пересечения отрезков AN и MC. L - точка пересечения отрезков BP и MC. Площадь треугольника ABC=1. Найти площадь четырехугольника AQLP. Найти значения чисел p и q, если AQ=pAB+qAL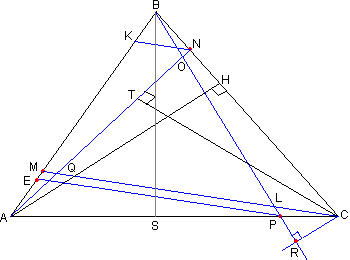

Из отношения BN:NC=1:4, получаем NC=4BN, а ВС=BN+NC=5BN или BN=1/4 * NC и ВС=BN+NC=5/4 * NC, откуда NC=4/5BC
Запишем формулу площади треугольника АВС:
S_ABC=1/2AH * ВС=1
S_ANC=1/2AH * NC=1/2AH * 4/5BC=4/5 * 1/2AH * ВС=4/5
Через точку N проведем прямую NK параллельно СМ. Из теоремы о том, что параллельные прямые отсекают на сторонах угла одинаковые отрезки, заключаем:
BM:KM=BC:NC=5BN:4BN=5/4, откуда КМ=4/5 * ВМ
Далее AQ:QN=АМ:КМ=АМ:4/5 * ВМ= =5/4 * АМ:ВМ=5/4 * 1/4=5/16, откуда QN=16/5AQ, а AN=AQ+QN=21/5AQ, откуда AQ=5/21 * AN
Запишем формулу площади треугольника ANC:
S_ANC=1/2CT * AN=4/5
S_AQC=1/2CT * AQ=1/2CT * 5/21 * AN
S_AQC=5/21 * 1/2CT * AN=5/21 * S_ANC=5/21 * 4/5=4/21

Через точку Р проведем прямую РЕ параллельно СМ. Из теоремы о том, что параллельные прямые отсекают на сторонах угла одинаковые отрезки, заключаем:
ЕМ:ЕА=СР:РА=1/4, откуда ЕА=4ЕМ, а АМ=АЕ+ЕМ=5ЕМ или ЕМ=1/5AM
По той же теореме ЕМ:ВМ=LP:BL или LP:BL=1/5AM:BM=1/5 * AM:BM=1/5 * 1/4=1/20, откуда BL=20LP, а ВР=BL+LP=21LP, значит:
LP=1/21 * BP

Из отношения CP:PA=1:4, получаем РА=4СР, а АС=РА+СР=5СР, откуда СР=1/5АС
Запишем формулу площади треугольника АВС:
S_ABC=1/2ВС * АС=1
S_ВРС=1/2BS * CР=1/2BS * 1/5АС=1/5 * 1/2BS * АС=1/5 * S_ABC=1/5

Запишем формулу площади треугольника ВРС:
S_ВРС=1/2CR * ВР=1/5
S_LCP=1/2CR * LP=1/2CR * 1/21 * BP=1/21 * 1/2CR * ВР=1/5 * 1/21=1/105

S_AQLP=S_AQC-S_LCP=4/21-1/105=19/105