| Главная Научный калькулятор | |
|
|
Задача №205В шар радиуса R вписан конус Найти объем конуса, если угол при вершине его осевого сечения равен 2α 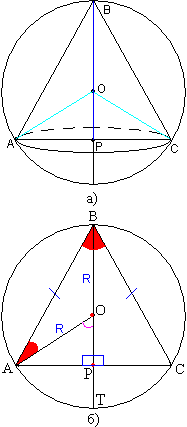 На рисунке а) изображен конус, вписанный в шар. Конус наш прямой круговой, т.е. его высота падает в центр основания. Большинство школьных(и не только) учебников под конусом понимают прямой круговой конус (если бы конус был общего вида, то известных условий не хватило бы для решения задачи).
На рисунке а) изображен конус, вписанный в шар. Конус наш прямой круговой, т.е. его высота падает в центр основания. Большинство школьных(и не только) учебников под конусом понимают прямой круговой конус (если бы конус был общего вида, то известных условий не хватило бы для решения задачи). Итак, прямой круговой конус (круговой - т.е. основание есть круг, окружность), вписанн в шар. Осевое сечение - это сечение проходящее через ось конуса или его высоту. Поведем любое осевое сечение данного конуса. Пусть оно пересечет его основание по диаметру АС (это диаметр, т.к. АС проходит через центр окружности - основание высоты по определению прямого кругового конуса). Определение. Плоскости называют перпендикулярными, если одна из них проходит через прямую, перпендикулярную второй плоскости. Поэтому плоскость АВС - плоскость осевого сечения перпендикулярна плоскости основания. Высота конуса проходит через центр этого шара. Доказательство: Из центра шара точки О опустим перпендикуляр ОР на основание конуса. Теорема. Если из точки, принадлежащей одной из двух перпендикулярных плоскостей, провести перпендикуляр к другой плоскости, то это перпендикуляр полностью лежит в первой плоскости. Эта теорема говорит нам, что точка Р лежит на АС и только на АС. Определение: прямая, перпендикулярная данной плоскости, перпендикулярна любой прямой в этой плоскости, т.е. ОР перпендикулярна АС. Соединим точки А с О и С с О. Треугольник АОС является равнобедренным по определению (ОА=ОС - радиусы шара равны). По свойству равнобедренного треугольника (высота (ОР является высотой треугольника по определению), проведенная к основанию равнобедренного треугольника является медианой и серединным перпендикуляром основания, биссектрисой угла при вершине, лежащей против основания) высота ОР является также медианой, и поэтому точка Р является серединой АС также, как и основание высоты конуса. Мы имеем два различных перпендикуляра, проходящих через одну точку Р, чего быть не может, поэтому эти перпендикуляры совпадают и перпендикуляр ОР лежит на высоте конуса, а частности и точка О - центр шара лежит. Рассмотрим осевое счечение АВС на рисунке б). Треугольники АВР и СВР являются прямоугольными, т.к. ВР - высота - образует с АС прямой угол (угол, смежный прямому углу, прямой). Эти треугольники равны по признаку равенства прямоугольных треугольников по двум катетам (ВР - общая, АР=СР - радиусы окружности - основания). Поэтому равны и гипотенузы этих треугольников АВ=ВС. Треугольник АВС является равнобедренным по определению (треугольник, две стороны которого равны, является равнобедренным). По свойству равнобедренного треугольника: высота (ВР является высотой треугольника по определению), проведенная к основанию равнобедренного треугольника является медианой и серединным перпендикуляром основания, биссектрисой (биссектриса делит угол пополам) угла при вершине, лежащей против основания, имеем ∠АВР=∠СВР=1/2∠АВС=1/2 * 2α=α Треугольник АОВ является равнобедренным по определению (ОА=ОВ - радиусы шара равны). Теорема: углы при основании равнобедренного треугольника равны, т.е. ∠АВО=∠ОАВ=α. Из теоремы о внешнем угле треугольника (внешний угол треугольника равен сумме двух внутренних, несмжных с ним), заключаем: ∠АОР=∠АВО+∠ВОА=2α Из прямоугольного треугольника АОР находим: ОР=R * cos2α AP=R * sin2α Найдем высоту конуса: ВР=ВО+ОР=R+R * cos2α=R(1+cos2α) Найдем площадь основания: АР - радиус основания, поэтому S=πAP2=π(R * sin2α)2 Найдем объем конуса: 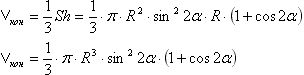
|