| Главная Научный калькулятор | |
|
|
1) Высота правильной четырехугольной пирамиды равна 4 см, а боковые грани образуют с основанием угол 45 градусов.
Найдите: площадь боковой поверхности пирамиды, угол между противолежащими боковыми гранями.
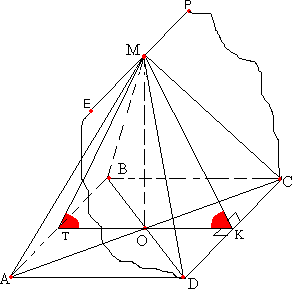 Пирамида правильная, значит, основание квадрат, а высота падает в его центр - точку пересечения диагоналей. Из точки О опусти перпендикуляр на CD. Соединим точки К и М. КМ перпендикулярна CD по теореме о трех перпендикулярах. Мы построили линейный угол двугранного угла между боковой гранью и основанием.
Пирамида правильная, значит, основание квадрат, а высота падает в его центр - точку пересечения диагоналей. Из точки О опусти перпендикуляр на CD. Соединим точки К и М. КМ перпендикулярна CD по теореме о трех перпендикулярах. Мы построили линейный угол двугранного угла между боковой гранью и основанием.Боковые грани правильной пирамиды суть равные равнобедренные треугольники, поэтому: Sбок=4SMCD Рассмотрим прямоугольный треугольник АМК. Найдем в нем катет и гипотенузу по известным катету и острому углу: 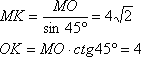 Рассмотрим прямоугольный треугольник ОКС. В нем угол ОСК равен 45° (по свойству диагонали квадрата - частного вида ромба), поэтому данный треугольник является равнобедренным (два угла по 45°), т.е. КС=ОК=4 Треугольник СОD является равнобедренным (OD=ОС - диагонали квадрата равны и точкой пересечения делятся пополам), поэтому, пользуясь свойством равнобедренного треугольника, доказываем, что выста ОК является также медианой, т.е. КС=KD, CD=2КС=8 Найдем площадь треугольника МСD: 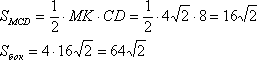 Продолжим отрезок ОК в сторону точки О до пересечения с АВ. Прямая КТ перпендикулярна АВ, т.к. она перпендикулярна CD по построению (если прямая перпендикулярна одной из двух (и более) параллельных прямых, то она перпендикулярна и второй (и остальным)). Соединим точки М и Т. МТ перпендикулярна АВ по теореме о трех перпендикулярах. Мы построили линейный угол двугранного угла между боковой гранью и основанием. Если прямая перпендикулярна плоскости, то она перпендикулярна любой прямой в этой плоскости (по определению), поэтому МО перпендикулярна ОТ и ОК, т.е. треугольники ТОМ и КОМ прямоугольные с острым углом 45°. Откуда находим: ∠ТМО=180°-90°-∠МТО=45° ∠КМО=180°-90°-∠МКО=45° ∠КМТ=∠ТМО+∠КМО=90° Теперь докажем, что угол КМТ является углом между противолежащими боковыми гранями АВМ и CDМ. Через точку М проведем прямую ЕР параллельно CD. Через параллельные прямые ЕР и CD проведем плоскость (параллельные прямые определяют плоскость, притом только одну). Плоскость ЕРСD содержит в себе три точки М, С и D плоскости боковой грани МСВ (три точки пространства, не лежащие на одной прямой, определяют плоскость, притом только одну), поэтому плоскости ЕРСD и МСD совпадают. МК перпендикулярна CD (по доказаннму), поэтому МК перпендикулярна ЕР (если прямая перпендикулярна одной из двух (и более) параллельных прямых, то она перпендикулярна и второй (и остальным)). Вспомним теорему: две прямые пространства, параллельные третей прямой, параллельны между собой. ЕР параллельна CD по построению, и АВ параллельна CD (противоположные стороны квадрата параллельны), поэтому АВ параллельна ЕР. Через параллельные прямые ЕР и CD проведем плоскость (параллельные прямые определяют плоскость, притом только одну). Плоскость ЕРВА содержит в себе три точки М, А и В плоскости боковой грани АВМ (три точки пространства, не лежащие на одной прямой, определяют плоскость, притом только одну), поэтому плоскости ЕРВА и АВМ совпадают. МТ перпендикулярна АВ (по доказаннму), поэтому МТ перпендикулярна ЕР (если прямая перпендикулярна одной из двух (и более) параллельных прямых, то она перпендикулярна и второй (и остальным)). Таким образом, мы имеем два перпендикуляра восстановленные из точки М в разных плоскотях, причем точка М лежит на ребре ЕР двугранного угла между плоскостями АВМ и МСD. Поэтому угол КМТ является линейным углом двугранного угда между между противолежащими боковыми гранями АВМ и CDМ. |