| Главная Научный калькулятор | |
|
|
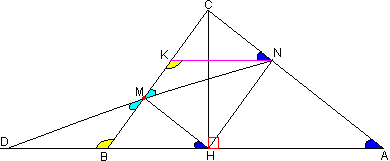
В треугольнике ABC со сторонами AB = 14, AC = 15, BC = 13 через основание высоты CH проводятся прямые, параллельные прямым АC и BC, которые пересекают соответственно стороны BC и AC треугольника в точках M и N. прямая MN пересекает продолжение стороны AB в точке D. Найти BD.
 Найдем угол треугольника при вершине В по теореме косинусов:
Найдем угол треугольника при вершине В по теореме косинусов: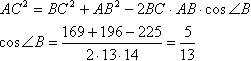 Теперь из прямоугольного треугольника ВСН найдем ВН Треугольники АВС и НВМ подобны по двум углам (угол В - общий, ∠ВНМ=∠ВАС равны как соответственные при параллельных прямых МН и АС и секущей АВ), поэтому найдем отношения: 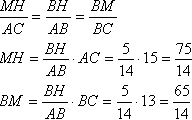 Четырехугольник МНNС является параллелограммом по определению (противоположные стороны параллельны), поэтому по свойству параллелограмма (противоположные стороны равны) МН=CN Через точку N проведем прямую параллельно АВ. Треугольники АВС и KCN подобны по двум углам (угол C - общий, ∠CNK=∠ВАС равны как соответственные при параллельных прямых KN и АВ и секущей АС), поэтому найдем отношения: 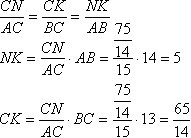 Найдем МК: МК=ВС-ВМ-СК=26/7 Треугольник МКN подобен треугольнику MBD по двум углам (∠BMD=∠КMN как вертикальные, ∠МВD=∠МКN как накрест лежащие для параллельных прямых АВ и KN и секущей ВС), поэтому найдем отношения: 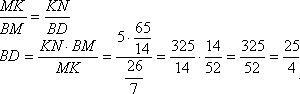
|