| Главная Научный калькулятор | |
|
|
Задача №217Диагональным сечением прямоугольного параллелепипеда, вписанного в шар, является квадрат площадью S. Найдите объём шара!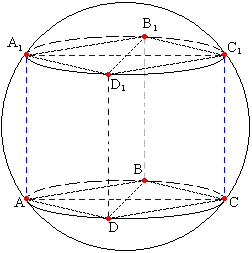 Любое сечение шара плоскостью есть круг, поэтому в сечении получаем квадрат АА1С1С вписанный в круг. 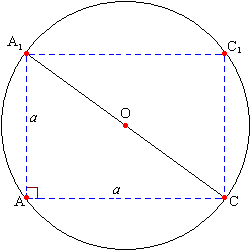 Проведем диагональ квадрата А1С. Прямой угол, вписанный в окружность, опирается на диаметр, поэтому гипотенуза А1С прямоугольного треугольника АА1С есть диаметр круга-сечения, а следовательно и самого шара. Произведем следующие действия: 1. Выразим сторону квадрата а через его известную площадь S; 2. Найдем диаметр круга-сечения по теореме Пифагора из прямоугольного треугольника АА1С; 3. Найдем радиус как половину диаметра; 4. Найдем объем шара. 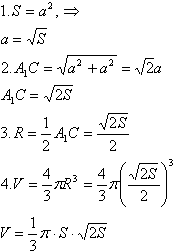
|